|
|
| Line 66: |
Line 66: |
| | <math>I=2I_1 + I_2=2\left(\frac{3\mathcal{E}}{4R}\right)+\frac{\mathcal{E}}{2R}=\frac {2\mathcal{E}}{R}</math> | | <math>I=2I_1 + I_2=2\left(\frac{3\mathcal{E}}{4R}\right)+\frac{\mathcal{E}}{2R}=\frac {2\mathcal{E}}{R}</math> |
| | | | |
| − | <math>R_{\textrm{eq}}=\frac{\mathcal{E}}{I}=\frac {5}{6}R</math> | + | <math>R_{\textrm{eq}}=\frac{\mathcal{E}}{I}=\frac {1}{2}R</math> |
| | | | |
| | ===(c)=== | | ===(c)=== |
| Line 77: |
Line 77: |
| | #<math>0=-2 I_1 R-I_2 R + \mathcal{E}</math> (loop rule abgda) | | #<math>0=-2 I_1 R-I_2 R + \mathcal{E}</math> (loop rule abgda) |
| | | | |
| − | <math>0=-2 I_1 R-½I_1 R + \mathcal{E} \rightarrow I_1=\frac{2\mathcal{E}}{5R}</math> | + | <math>0=-2 I_1 R-\frac {1}{2}I_1 R + \mathcal{E} \rightarrow I_1=\frac{2\mathcal{E}}{5R}</math> |
| | | | |
| | <math>I=3I_1=\frac{6\mathcal{E}}{5R}</math> | | <math>I=3I_1=\frac{6\mathcal{E}}{5R}</math> |
| | + | |
| | + | <math>R_{\textrm{eq}}=\frac{\mathcal{E}}{I}=\frac {5}{6}R</math> |
Revision as of 23:44, 30 March 2019
Problem
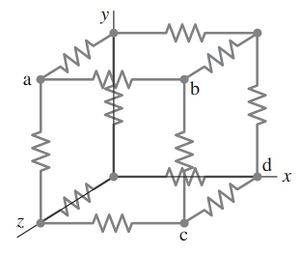
Twelve resistors, each of resistance R, are connected as the edges of a cube. Determine the equivalent resistance
(a) between points a and b, the ends of a side;
(b) between points a and c, the ends of a face diagonal;
(c) between points a and d, the ends of the volume diagonal.
[Hint: Apply an emf and determine currents; use symmetry at junctions.]
solution
(a)
Insert a probe battery between points (a) and (b). Let's label the current drawn from this probe battery as I
This setup has a symmetry plane between abed, so the current split at junction a will be 
Another symmetry is that the afhe plane is the mirror cdgb (since one has the current I entering, and the other has the current leaving) thus we have the same currents in erverse directions in those planes.
The 6 equations in the symmetry reduced cube is:






6 equations and 6 unknowns, so we start solving:
 (2 and 6 in 1)
(2 and 6 in 1) (2 and 6 in 4)
(2 and 6 in 4) (3 in 5)
(3 in 5)
 ( solution of 3)
( solution of 3)
 (previous into 2)
(previous into 2)
 (previous into 1)
(previous into 1)

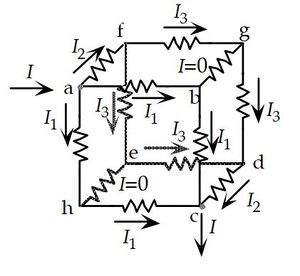
(b)
Insert a probe battery between points (a) and (c). Let's label the current drawn from this probe battery as I
This ehgb is a symmetry (inversion) plane afcd is a symmmetry plane.
 (Junction rule at a)
(Junction rule at a) (Junction rule at d)
(Junction rule at d) (loop rule around abca)
(loop rule around abca) (loop rule around afgdcha)
(loop rule around afgdcha)
Then





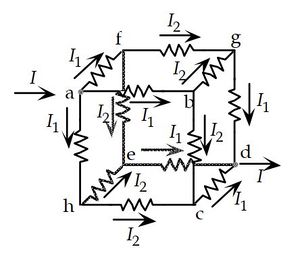
(c)
Insert a probe battery between points (a) and (d). Let's label the current drawn from this probe battery as I
 (junction rule at a)
(junction rule at a) (junction rule at b)
(junction rule at b) (loop rule abgda)
(loop rule abgda)