Difference between revisions of "Chapter 28 Problem 24"
From 105/106 Lecture Notes by OBM
(Created page with "==Problem== thumb|right|Current loop and wire A triangular loop of side length a carries a current <math>I</math>. If this loop is placed a di...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | [[File:Chapter28Problem24q.png| | + | [[File:Chapter28Problem24q.png|300px|center|Current loop and wire]] |
A triangular loop of side length a carries a current <math>I</math>. If this loop is placed a distance <math>d</math> away from a very long straight wire carrying a current <math>I^\prime</math>,determine the force on the loop. | A triangular loop of side length a carries a current <math>I</math>. If this loop is placed a distance <math>d</math> away from a very long straight wire carrying a current <math>I^\prime</math>,determine the force on the loop. | ||
==Solution== | ==Solution== | ||
| + | [[File:Chapter28Problem24s.png|500px|center|Forces and distances]] | ||
The current in the parallel branch flows in the same direction as the long straight wire, so the force is attractive with magnitude: | The current in the parallel branch flows in the same direction as the long straight wire, so the force is attractive with magnitude: | ||
| Line 10: | Line 11: | ||
By symmetry the magnetic force for the other two segments will be equal. | By symmetry the magnetic force for the other two segments will be equal. | ||
| − | <math> | + | <math>F_{2y}=\int_0^{a/2}\frac{\mu_0 I I^\prime}{2\pi \left(d+\sqrt{3}x\right)}dx=\frac{\mu_0 I I^\prime}{2\pi\sqrt{3}}\left. \ln\left(d+\sqrt{3}x\right) \right|_0^{a/2}</math> |
| + | <math>=\frac{\mu_0 I I^\prime}{2\pi\sqrt{3}} \ln\left(1+\frac{\sqrt{3}a}{2d}\right) </math> | ||
| + | |||
| + | The magnitude of the net force is: | ||
| + | |||
| + | <math>F_1-2F_{2y}=\frac{\mu_0 I I^\prime}{\pi} \left [\frac{a}{2d}-\frac{\sqrt{3}}{3}\ln\left(1+\frac{\sqrt{3}a}{2d}\right)\right]</math> | ||
Latest revision as of 06:48, 16 April 2019
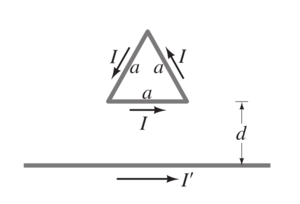
Problem
A triangular loop of side length a carries a current . If this loop is placed a distance away from a very long straight wire carrying a current ,determine the force on the loop.
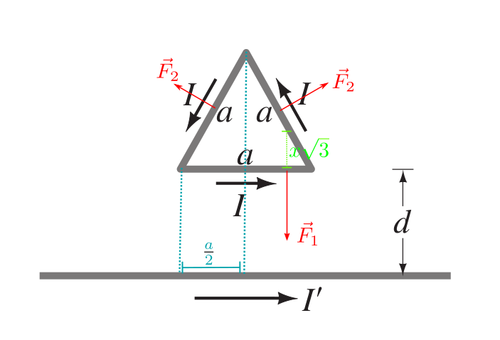
Solution
The current in the parallel branch flows in the same direction as the long straight wire, so the force is attractive with magnitude:
By symmetry the magnetic force for the other two segments will be equal.
The magnitude of the net force is:






![{\displaystyle F_{1}-2F_{2y}={\frac {\mu _{0}II^{\prime }}{\pi }}\left[{\frac {a}{2d}}-{\frac {\sqrt {3}}{3}}\ln \left(1+{\frac {{\sqrt {3}}a}{2d}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96d20aea345753354f2d12f92d94827b7e48aa6b)