Chapter 30 Problem 13

Problem

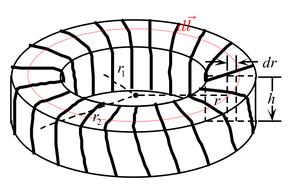
A toroid has a rectangular cross section. Show that the self-inductance is

$L={\frac {\mu _{0}N^{2}h}{2\pi }}\ln {\frac {r_{2}}{r_{1}}}$

where $N$ is the total number of turns and $r_{1}$ , $r_{2}$ , and $h$ are shown above. [Hint: Use Ampère’s law to get $B$ as a function of $r$ inside the toroid, and integrate.]

Solution

Magnetic field inside as a function of $r$:

$\oint {\vec {B}}.d{\vec {l}}=\mu _{0}I_{\textrm {encl}}$

Failed to parse (syntax error): {\displaystyle B (2 \pi r)=\mu_0 NI}}

$B={\frac {\mu _{0}NI}{(2\pi r)}}$

the self-inductance is related to the flux is the integral of the magnetic field over a cross-section of the toroid.

$L={\frac {N\Phi _{B}}{I}}={\frac {N}{I}}\int _{r_{1}}^{r_{2}}{\frac {\mu _{0}NI}{(2\pi r)}}hdr={\frac {\mu _{0}N^{2}h}{2\pi }}\ln {\frac {r_{2}}{r_{1}}}$