Difference between revisions of "Chapter 30 Problem 26"
From 105/106 Lecture Notes by OBM
(Created page with "==Problem== 300px|center|A LR circuit In this circuit, determine the current in each resistor <math>I_1</math> , <math>I_2</math> , <math>I_3...") |
|||
| Line 13: | Line 13: | ||
(d) after a long time? | (d) after a long time? | ||
| + | |||
| + | |||
| + | ==Solution== | ||
| + | ===(a)=== | ||
| + | At the moment the switch is closed, no current will flow through the inductor. Therefore, the resistors <math>R_1</math> and <math>R_2</math> can be treated as in series. | ||
| + | |||
| + | <math>\mathcal{E}=I(R_1+R_2)\rightarrow I_1=I_2=\frac{\mathcal{E}}{R_1+R_2},I_3=0</math> | ||
| + | |||
| + | ===(b)=== | ||
| + | A long time after the switch is closed, there is no voltage drop across the inductor so resistors <math>R_2</math> and <math>R_3</math> can be treated as parallel resistors in series with <math>R_1</math> . | ||
| + | |||
| + | <math>I_1=I_2+I_3</math> | ||
| + | |||
| + | <math>\mathcal{E}=I_1 R_1+ I_2 R_2</math> | ||
| + | |||
| + | <math>I_2 R_2 = I_3 R_3</math> | ||
| + | |||
| + | <math>\frac{\mathcal{E}-I_2 R_2}{R_1}=I_2 + \frac{I_2 R_2}{R_3}</math> | ||
| + | |||
| + | |||
| + | <math>I_2=\frac{\mathcal{E}R_3}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
| + | |||
| + | <math>I_3=\frac{I_2 R_2}{R_3}= \frac{\mathcal{E}R_2}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
| + | |||
| + | <math>I_1=I_2+I_3=\frac{\mathcal{E}(R_3+R_2)}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
Revision as of 23:08, 5 May 2019
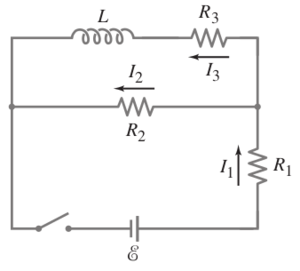
Problem
In this circuit, determine the current in each resistor , , at the moment
(a) the switch is closed,
(b) a long time after the switch is closed.
After the switch has been closed for a long time, and then reopened, what is each current
(c) just after it is opened,
(d) after a long time?
Solution
(a)
At the moment the switch is closed, no current will flow through the inductor. Therefore, the resistors and can be treated as in series.
(b)
A long time after the switch is closed, there is no voltage drop across the inductor so resistors and can be treated as parallel resistors in series with .