Difference between revisions of "Chapter 25 Problem 30"
From 105/106 Lecture Notes by OBM
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
==Problem== | ==Problem== | ||
| − | [[File:Chapter25problem30q.png| | + | [[File:Chapter25problem30q.png|400 px|center|The resistor]] |
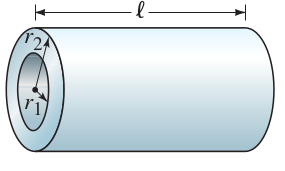
A hollow cylindrical resistor with inner radius <math>r_1</math> and outer radius <math>r_2</math> , and length <math>l</math> , is made of a material whose resistivity is <math>\rho</math> | A hollow cylindrical resistor with inner radius <math>r_1</math> and outer radius <math>r_2</math> , and length <math>l</math> , is made of a material whose resistivity is <math>\rho</math> | ||
| Line 9: | Line 10: | ||
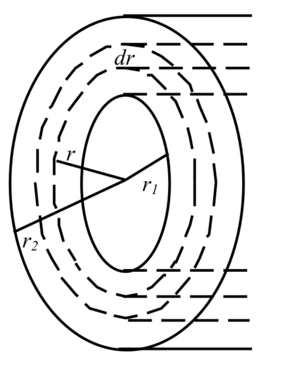
for current that flows radially outward. [Hint: Divide the resistor into concentric cylindrical shells and integrate.] | for current that flows radially outward. [Hint: Divide the resistor into concentric cylindrical shells and integrate.] | ||
| − | (b) Evaluate the resistance <math>R</math> for such a resistor made of carbon whose inner and outer radii are 1.0 mm and 1.8 mm and whose length is 2.4 cm | + | (b) Evaluate the resistance <math>R</math> for such a resistor made of carbon whose inner and outer radii are 1.0 mm and 1.8 mm and whose length is 2.4 cm (Choose <math>\rho = 15 \times 10^{-5}\Omega\cdot m</math>.) |
(c) What is the resistance in part (b) for current flowing parallel to the axis? | (c) What is the resistance in part (b) for current flowing parallel to the axis? | ||
| Line 18: | Line 19: | ||
<math>dR=\rho\frac{dr}{2\pi r l}</math> | <math>dR=\rho\frac{dr}{2\pi r l}</math> | ||
| − | <math>R=\int dR=\ | + | <math>R=\int dR=\int_{r_1}^{r_2} \rho \frac{dr}{2\pi r l}=\frac{\rho}{2\pi l}\ln\frac{r_2}{r_1}</math> |
| + | ===(b)=== | ||
| + | <math>R=\frac{15 \times 10^{-5}\Omega\cdot \textrm{m}}{2\pi(0.024 \textrm{m})}\ln\left(\frac{1.8\textrm{mm}}{1.0\textrm{mm}}\right)=5.8\times10^{-4}\Omega</math> | ||
| − | ===( | + | ===(c)=== |
| + | |||
| + | <math>R=\frac{\rho l}{A}=\frac{\rho l}{\pi (r_2^2-r_1^2)}=\frac{(15 \times 10^{-5}\Omega\cdot \textrm{m})(0.024 \textrm{m})}{\pi\left[(1.8\times10^{-3}\textrm{m})^2-(1.0\times10^{-3}\textrm{m})^2\right]}=0.51\Omega</math> | ||
Latest revision as of 21:32, 6 April 2020
Problem
A hollow cylindrical resistor with inner radius and outer radius , and length , is made of a material whose resistivity is
(a) Show that the resistance is given by
for current that flows radially outward. [Hint: Divide the resistor into concentric cylindrical shells and integrate.]
(b) Evaluate the resistance for such a resistor made of carbon whose inner and outer radii are 1.0 mm and 1.8 mm and whose length is 2.4 cm (Choose .)
(c) What is the resistance in part (b) for current flowing parallel to the axis?
Solution
(a)
(b)
(c)










![{\displaystyle R={\frac {\rho l}{A}}={\frac {\rho l}{\pi (r_{2}^{2}-r_{1}^{2})}}={\frac {(15\times 10^{-5}\Omega \cdot {\textrm {m}})(0.024{\textrm {m}})}{\pi \left[(1.8\times 10^{-3}{\textrm {m}})^{2}-(1.0\times 10^{-3}{\textrm {m}})^{2}\right]}}=0.51\Omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/66dcdd7018daf982f83d0d1c03d67b3ba33d4e52)