Difference between revisions of "Chapter 26 Problem 71"
From 105/106 Lecture Notes by OBM
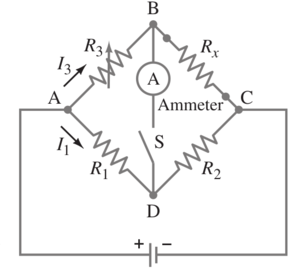
(Created page with "==Problem== thumb|right|The Wheatstone bridge A '''Wheatstone bridge''' is a type of “bridge circuit” used to make measurements of resista...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
==Problem== | ==Problem== | ||
[[File:Chapter26problem71q.png|thumb|right|The Wheatstone bridge]] | [[File:Chapter26problem71q.png|thumb|right|The Wheatstone bridge]] | ||
| Line 11: | Line 12: | ||
No current means the potential difference between B and D is zero. Thus | No current means the potential difference between B and D is zero. Thus | ||
| − | <math>V_{\textrm{BA}}= | + | <math>V_{\textrm{BA}}=V_{\textrm{DA}}</math> |
<math>\rightarrow I_3 R_3= I_1 R_1 </math> | <math>\rightarrow I_3 R_3= I_1 R_1 </math> | ||
<math>\rightarrow \frac{R_3}{R_1}= \frac{I_1}{I_3} </math> | <math>\rightarrow \frac{R_3}{R_1}= \frac{I_1}{I_3} </math> | ||
| − | <math>V_{\textrm{CB}}= | + | <math>V_{\textrm{CB}}=V_{\textrm{CD}}</math> |
<math>\rightarrow I_3 R_x= I_1 R_2 </math> | <math>\rightarrow I_3 R_x= I_1 R_2 </math> | ||
<math>\rightarrow R_x=R_2\frac{I_1}{I_3}= \frac{R_2 R_3}{R_1} </math> | <math>\rightarrow R_x=R_2\frac{I_1}{I_3}= \frac{R_2 R_3}{R_1} </math> | ||
Latest revision as of 15:02, 17 April 2020
Problem
A Wheatstone bridge is a type of “bridge circuit” used to make measurements of resistance. The unknown resistance to be measured, , is placed in the circuit with accurately known resistances , , and . One of these, , is a variable resistor which is adjusted so that when the switch is closed momentarily, the ammeter A shows a zero current flow.
(a) Determine in terms of , , and .
(b) If a Wheatstone bridge is “balanced” when , , and , what is the value of the unknown resistance?
Solution
(a)
No current means the potential difference between B and D is zero. Thus
(b)