Difference between revisions of "Chapter 29 Problem 33"
From 105/106 Lecture Notes by OBM
(Created page with "==Problem== 300px|center|Rail in a magnetic field A conducting rod rests on two long frictionless parallel rails in a magnetic field <math>\v...") |
m |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
==Problem== | ==Problem== | ||
[[File:Chapter29Problem33q.png|300px|center|Rail in a magnetic field]] | [[File:Chapter29Problem33q.png|300px|center|Rail in a magnetic field]] | ||
| Line 7: | Line 8: | ||
(b) Suppose at <math>t = 0</math>, when the rod has speed <math>v = v_0</math> , the two rails are connected electrically by a wire from point a to point b. Assuming the rod has resistance <math>R</math> and the rails have negligible resistance, determine the speed of the rod as a function of time. Discuss your answer. | (b) Suppose at <math>t = 0</math>, when the rod has speed <math>v = v_0</math> , the two rails are connected electrically by a wire from point a to point b. Assuming the rod has resistance <math>R</math> and the rails have negligible resistance, determine the speed of the rod as a function of time. Discuss your answer. | ||
| + | |||
| + | ==Solution== | ||
| + | |||
| + | ===(a)=== | ||
| + | yes, the rod travels at constant speed. | ||
| + | |||
| + | Changing flux would cause an emf across the rod, but no current can flow. Without the current, there is no force to oppose the motion of the rod. | ||
| + | |||
| + | ===(b)=== | ||
| + | [[File:Chapter29Problem33s.png|300px|center|As the rod moves]] | ||
| + | |||
| + | <math> \mathcal{E}=-\frac{d\Phi_B}{dt}=-\frac{BdA}{dt}=-\frac{Blvdt}{dt}=-Blv</math> | ||
| + | |||
| + | <math> I=\frac{\mathcal{E}}{R}=-\frac{Blv}{R}</math> | ||
| + | |||
| + | <math>F=ma=m\frac{dv}{dt}=IlB=-\frac{B^2l^2}{R}v</math> | ||
| + | |||
| + | <math>\rightarrow\frac{dv}{v}=-\frac{B^2l^2}{mR}dt</math> | ||
| + | |||
| + | <math>\int_{v_0}^{v}\frac{dv^\prime}{v^\prime}=-\frac{B^2l^2}{mR}\int_0^t dt^\prime</math> | ||
| + | <math>\rightarrow \ln \frac{v}{v_0}=-\frac{B^2l^2}{mR}t</math> | ||
| + | |||
| + | <math>v(t)=v_0 e^{-\frac{B^2l^2}{mR}t}</math> | ||
Latest revision as of 22:33, 10 May 2020
Problem
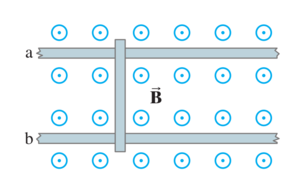
A conducting rod rests on two long frictionless parallel rails in a magnetic field ( to the rails and rod)
(a) If the rails are horizontal and the rod is given an initial push, will the rod travel at constant speed even though a magnetic field is present?
(b) Suppose at , when the rod has speed , the two rails are connected electrically by a wire from point a to point b. Assuming the rod has resistance and the rails have negligible resistance, determine the speed of the rod as a function of time. Discuss your answer.
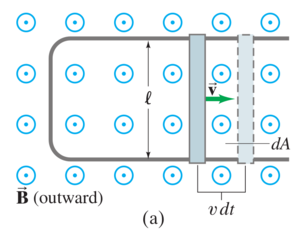
Solution
(a)
yes, the rod travels at constant speed.
Changing flux would cause an emf across the rod, but no current can flow. Without the current, there is no force to oppose the motion of the rod.
(b)