Difference between revisions of "Chapter 22 Problem 30"
From 105/106 Lecture Notes by OBM
(→(c)) |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
==Problem== | ==Problem== | ||
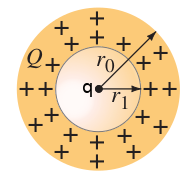
[[File:Chapter22-problem30q.png|thumb|right|Non-conducting sphere with a charge inside]] | [[File:Chapter22-problem30q.png|thumb|right|Non-conducting sphere with a charge inside]] | ||
| Line 17: | Line 18: | ||
<math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q</math> | <math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q</math> | ||
| − | <math>E_q=\frac{q}{4\pi\ | + | <math>E_q=\frac{q}{4 \pi \epsilon_0 r^2}</math> (radially pointing from the charge) |
| − | <math>E_\textrm{sphere}\rightarrow \oint \vec{E} \cdot d\vec{A}=E(4\pi | + | <math>E_\textrm{sphere}\rightarrow \oint \vec{E} \cdot d\vec{A}=E(4\pi r^2)=\frac{Q_\textrm{encl}}{\epsilon_0}</math> (radial direction) |
<math>E_\textrm{sphere}=\frac{Q_\textrm{encl}}{4\pi\epsilon_0 r^2}</math> | <math>E_\textrm{sphere}=\frac{Q_\textrm{encl}}{4\pi\epsilon_0 r^2}</math> | ||
so the question is about finding the <math>Q_\textrm{encl}</math> | so the question is about finding the <math>Q_\textrm{encl}</math> | ||
| + | |||
| + | ===(a)=== | ||
| + | <math>E_\textrm{sphere}=0</math> | ||
| + | |||
| + | <math>\vec{E}_T=\vec{E}_q=\frac{q}{4 \pi \epsilon_0 r^2}\hat{r}</math> | ||
| + | |||
| + | ===(b)=== | ||
| + | First, let's calculate the uniform charge density <math>\rho</math> in terms of the charge held by the shell <math>Q_\textrm{shell}</math>. | ||
| + | |||
| + | <math>Q_\textrm{shell}=\rho\left(\frac{4}{3}\pi r_0^3 - \frac{4}{3}\pi r_1^3 \right)</math> | ||
| + | |||
| + | <math>\rho=\frac{3Q_\textrm{shell}}{4\pi(r_0^3 - r_1^3 )} </math> | ||
| + | |||
| + | using this, we can calculate <math>Q_\textrm{encl}</math> | ||
| + | |||
| + | <math>E_\textrm{sphere}=\frac{Q_\textrm{encl}}{4\pi\epsilon_0 r^2}=\frac{\rho\left[\frac{4}{3}\pi r^3 - \frac{4}{3}\pi r_1^3 \right]}{4\pi\epsilon_0 r^2}</math> | ||
| + | |||
| + | <math>=\frac{Q_\textrm{sphere}}{4\pi\epsilon_0 r^2}\frac{r^3-r_1^3}{r_0^3-r_1^3}</math> | ||
| + | |||
| + | <math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q=\frac{1}{4\pi\epsilon_0 r^2}\left[q+Q_\textrm{sphere}\frac{r^3-r_1^3}{r_0^3-r_1^3}\right]\hat{r}</math> | ||
| + | |||
| + | ===(c)=== | ||
| + | This is straightforward using Gauss's law and a surface that encompasses all the charges outside the shell | ||
| + | |||
| + | <math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q=\frac{Q_\text{sphere}+q}{4\pi\epsilon_0 r^2}\hat{r}</math> | ||
Latest revision as of 09:39, 18 February 2020
Problem
A nonconducting sphere has a spherical cavity of radius centered at the sphere’s center. Assuming the charge is distributed uniformly in the “shell” (between and ), determine the electric field as a function of for
(a)
(b)
(c)
Solution
Superposition principle
(radially pointing from the charge)
(radial direction)
so the question is about finding the
(a)
(b)
First, let's calculate the uniform charge density in terms of the charge held by the shell .
using this, we can calculate
(c)
This is straightforward using Gauss's law and a surface that encompasses all the charges outside the shell



















![{\displaystyle E_{\textrm {sphere}}={\frac {Q_{\textrm {encl}}}{4\pi \epsilon _{0}r^{2}}}={\frac {\rho \left[{\frac {4}{3}}\pi r^{3}-{\frac {4}{3}}\pi r_{1}^{3}\right]}{4\pi \epsilon _{0}r^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97278c8d467fb279677dde2b2805ffc741aaa8fc)

![{\displaystyle {\vec {E}}_{T}={\vec {E}}_{\textrm {sphere}}+{\vec {E}}_{q}={\frac {1}{4\pi \epsilon _{0}r^{2}}}\left[q+Q_{\textrm {sphere}}{\frac {r^{3}-r_{1}^{3}}{r_{0}^{3}-r_{1}^{3}}}\right]{\hat {r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d086cf2bc32ab96d0572b8cda435b070917a361)
