Difference between revisions of "106-2018192 Practice for Midterm 2"
m (Obm moved page Practice for Midterm 2 to 106-2018192 Practice for Midterm 2) |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
b) Draw the charging voltage curve through the capacitor, with the time constant and the maximum voltage numerically and clearly indicated. | b) Draw the charging voltage curve through the capacitor, with the time constant and the maximum voltage numerically and clearly indicated. | ||
| − | Tip: Thévenin equivalent circuit approach greatly simplifies this problem, if you know how. | + | Tip: Thévenin equivalent circuit approach greatly simplifies this problem, if you know how. |
| + | |||
| + | [https://www.electronics-tutorials.ws/dccircuits/dcp_7.html Thevenins Theorem Tutorial] | ||
| Line 19: | Line 21: | ||
(a) For the <math>\vec{E}</math> field, we found that the boundary condition at the interface of the superconductor is that <math>\vec{E}</math> must be normal to the surface, or in other words, that the tangential component must be zero. What is the analogous boundary condition for the magnetic field? | (a) For the <math>\vec{E}</math> field, we found that the boundary condition at the interface of the superconductor is that <math>\vec{E}</math> must be normal to the surface, or in other words, that the tangential component must be zero. What is the analogous boundary condition for the magnetic field? | ||
| − | [[File:106MT2-superconductor-v1.png|thumb|right| | + | [[File:106MT2-superconductor-v1.png|thumb|right|Current loop on top of a superconducting plate]] |
A small current loop with its magnetic moment <math>\vec{\mu}</math> oriented at an angle <math>\theta</math> from the normal, is located at a distance <math>d</math> from an infinite, superconducting sheet. | A small current loop with its magnetic moment <math>\vec{\mu}</math> oriented at an angle <math>\theta</math> from the normal, is located at a distance <math>d</math> from an infinite, superconducting sheet. | ||
| Line 30: | Line 32: | ||
(e) Find the force, as a function of <math>\theta</math>, towards or away from the superconductor. | (e) Find the force, as a function of <math>\theta</math>, towards or away from the superconductor. | ||
| + | |||
| + | |||
| + | |||
| + | [[106MT2Pr-solutions|solutions]] | ||
Latest revision as of 19:37, 24 September 2019
Disclaimer: These are some random questions which does not have anything to do with the exam. I have no idea or any say about exam questions.
Question 1
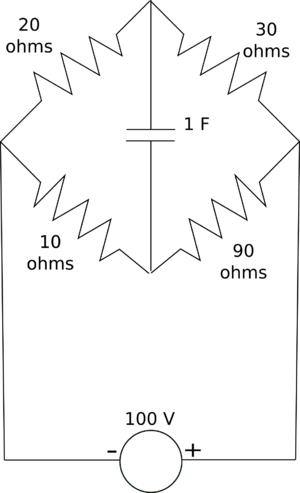
With the circuit parameters as specified and empty initial charge on the capacitor:
a) Determine the initial current through the capacitor in the instant you switch the power supply on.
b) Draw the charging voltage curve through the capacitor, with the time constant and the maximum voltage numerically and clearly indicated.
Tip: Thévenin equivalent circuit approach greatly simplifies this problem, if you know how.
Question 2
A superconducting metal has the property that inside the superconductor both and is zero.
(a) For the field, we found that the boundary condition at the interface of the superconductor is that must be normal to the surface, or in other words, that the tangential component must be zero. What is the analogous boundary condition for the magnetic field?
A small current loop with its magnetic moment oriented at an angle from the normal, is located at a distance from an infinite, superconducting sheet.
(b) Outline in a few sentences a method for finding the magnetic field everywhere, assuming that you already what the field of a magnetic dipole is.
(c) Find the torque on the dipole as a function of the angle
(d) Deduce the equilibrium angles. Which are stable, which unstable?
(e) Find the force, as a function of , towards or away from the superconductor.