Difference between revisions of "Chapter 30 Problem 26"
(Created page with "==Problem== 300px|center|A LR circuit In this circuit, determine the current in each resistor <math>I_1</math> , <math>I_2</math> , <math>I_3...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
==Problem== | ==Problem== | ||
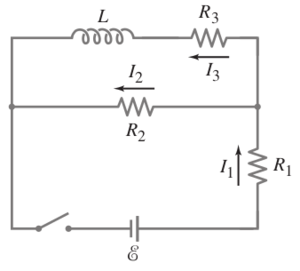
[[File:Chapter30Problem26q.png|300px|center|A LR circuit]] | [[File:Chapter30Problem26q.png|300px|center|A LR circuit]] | ||
| Line 13: | Line 14: | ||
(d) after a long time? | (d) after a long time? | ||
| + | |||
| + | |||
| + | ==Solution== | ||
| + | ===(a)=== | ||
| + | At the moment the switch is closed, no current will flow through the inductor. Therefore, the resistors <math>R_1</math> and <math>R_2</math> can be treated as in series. | ||
| + | |||
| + | <math>\mathcal{E}=I(R_1+R_2)\rightarrow I_1=I_2=\frac{\mathcal{E}}{R_1+R_2},I_3=0</math> | ||
| + | |||
| + | ===(b)=== | ||
| + | A long time after the switch is closed, there is no voltage drop across the inductor so resistors <math>R_2</math> and <math>R_3</math> can be treated as parallel resistors in series with <math>R_1</math> . | ||
| + | |||
| + | <math>I_1=I_2+I_3</math> | ||
| + | |||
| + | <math>\mathcal{E}=I_1 R_1+ I_2 R_2</math> | ||
| + | |||
| + | <math>I_2 R_2 = I_3 R_3</math> | ||
| + | |||
| + | <math>\frac{\mathcal{E}-I_2 R_2}{R_1}=I_2 + \frac{I_2 R_2}{R_3}</math> | ||
| + | |||
| + | |||
| + | <math>I_2=\frac{\mathcal{E}R_3}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
| + | |||
| + | <math>I_3=\frac{I_2 R_2}{R_3}= \frac{\mathcal{E}R_2}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
| + | |||
| + | <math>I_1=I_2+I_3=\frac{\mathcal{E}(R_3+R_2)}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
| + | |||
| + | ===(c)=== | ||
| + | Just after the switch is opened the current through the inductor continues with the same magnitude and direction. With the open switch, no current can flow through the branch with the switch. Therefore the current through <math>R_2</math> must be equal to the current through <math>R_3</math> , but in the opposite direction. | ||
| + | |||
| + | <math>I_3=\frac{\mathcal{E}R_2}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
| + | |||
| + | <math>I_2=\frac{-\mathcal{E}R_2}{R_2 R_3 + R_1 R_3 +R_1 R_2}</math> | ||
| + | |||
| + | <math>I_1=0</math> | ||
| + | |||
| + | ===(d)=== | ||
| + | After a long time, with no voltage source, the energy in the inductor will dissipate and no current will flow through any of the branches. | ||
| + | |||
| + | <math>I_1=I_2=I_3=0</math> | ||
Latest revision as of 23:12, 5 May 2019
Problem
In this circuit, determine the current in each resistor , , at the moment
(a) the switch is closed,
(b) a long time after the switch is closed.
After the switch has been closed for a long time, and then reopened, what is each current
(c) just after it is opened,
(d) after a long time?
Solution
(a)
At the moment the switch is closed, no current will flow through the inductor. Therefore, the resistors and can be treated as in series.
(b)
A long time after the switch is closed, there is no voltage drop across the inductor so resistors and can be treated as parallel resistors in series with .
(c)
Just after the switch is opened the current through the inductor continues with the same magnitude and direction. With the open switch, no current can flow through the branch with the switch. Therefore the current through must be equal to the current through , but in the opposite direction.
(d)
After a long time, with no voltage source, the energy in the inductor will dissipate and no current will flow through any of the branches.