Difference between revisions of "Practice 060519"
(Created page with "__NOTOC__ '''Disclaimer:''' These are some random questions which does not have anything to do with the exam. I have no idea or any say about exam questions. ==Question 1==...") |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
==Question 1== | ==Question 1== | ||
The liquid-drop model of the nucleus suggests that high-energy oscillations of certain nuclei can split (“fission”) a large nucleus into two unequal fragments plus a few neutrons. Using this model, consider the case of a uranium nucleus fissioning into two spherical fragments, one with a charge <math>q_1 = +38</math> e and radius <math>r_1 = 5.5 \times 10^{-15}</math> m, the other with <math>q_2 = + 54</math> e and <math>r_2 = 6.2 \times 10^{-15}</math> m. Calculate the electric potential energy (MeV) of these fragments, assuming that the charge is uniformly distributed throughout the volume of each spherical nucleus and that their surfaces are initially in contact at rest. The electrons surrounding the nuclei can be neglected. This electric potential energy will then be entirely converted to kinetic energy as the fragments repel each other. How does your predicted kinetic energy of the fragments agree with the observed value associated with uranium fission (approximately 200 MeV total)? [1 MeV = <math>10^6</math> eV]. | The liquid-drop model of the nucleus suggests that high-energy oscillations of certain nuclei can split (“fission”) a large nucleus into two unequal fragments plus a few neutrons. Using this model, consider the case of a uranium nucleus fissioning into two spherical fragments, one with a charge <math>q_1 = +38</math> e and radius <math>r_1 = 5.5 \times 10^{-15}</math> m, the other with <math>q_2 = + 54</math> e and <math>r_2 = 6.2 \times 10^{-15}</math> m. Calculate the electric potential energy (MeV) of these fragments, assuming that the charge is uniformly distributed throughout the volume of each spherical nucleus and that their surfaces are initially in contact at rest. The electrons surrounding the nuclei can be neglected. This electric potential energy will then be entirely converted to kinetic energy as the fragments repel each other. How does your predicted kinetic energy of the fragments agree with the observed value associated with uranium fission (approximately 200 MeV total)? [1 MeV = <math>10^6</math> eV]. | ||
| + | |||
| + | ==Question 2== | ||
| + | [[File:Exercise060519Problem2q2.jpg|500px|center|Atom trap]] | ||
| + | [[File:Exercise060519Problem2q3.png|300px|center|Atom trap]] | ||
| + | [[File:Exercise060519Problem2q1.png|300px|center|Atom trap]] | ||
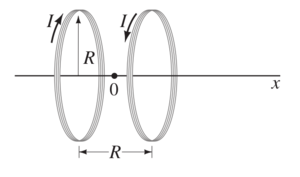
| + | The design of a magneto-optical atom trap requires a magnetic field <math>B</math> that is directly proportional to position <math>x</math> along an axis. Such a field perturbs the absorption of laser light by atoms in the manner needed to spatially confine atoms in the trap. Let us demonstrate that “anti-Helmholtz” coils will provide the required field <math>B = Cx</math>, where <math>C</math> is a constant. Anti-Helmholtz coils consist of two identical circular wire coils, each with radius <math>R</math> and <math>N</math> turns, carrying current <math>I</math> in opposite directions. The coils share a common axis (defined as the <math>x</math> axis with <math>x = 0</math> at the midpoint (0) between the coils). Assume that the centers of the coils are separated by a distance equal to the radius <math>R</math> of the coils. | ||
| + | |||
| + | (a) Show that the magnetic field at position <math>x</math> along the <math>x</math> axis is given by | ||
| + | |||
| + | <math>B(x)=\frac{4\mu_0 NI}{R}\left\{\left[4+\left(1-\frac{2x}{R}\right)^2\right]^{-\frac{3}{2}}-\left[4+\left(1+\frac{2x}{R}\right)^2\right]^{-\frac{3}{2}}\right\}</math> | ||
| + | |||
| + | (b)For small excursions from the origin where <math>\left|x\right| \ll R</math>, show that the magnetic field is given by <math>B \approx Cx</math>, where the constant <math>C = 48 \mu_0 NI/25\sqrt{5} R^2</math>. | ||
| + | |||
| + | (c) For optimal atom trapping, <math>dB/dx</math> should be about 0.15 T/m. Assume an atom trap uses anti-Helmholtz coils with <math>R</math> = 4.0 cm and <math>N</math> = 150. What current should flow through the coils? [Coil separation equal to coil radius, as assumed in this problem, is not a strict requirement for anti-Helmholtz coils.] | ||
| + | |||
| + | |||
| + | [[Solutions 060519|solutions]] | ||
Latest revision as of 06:09, 6 May 2019
Disclaimer: These are some random questions which does not have anything to do with the exam. I have no idea or any say about exam questions.
Question 1
The liquid-drop model of the nucleus suggests that high-energy oscillations of certain nuclei can split (“fission”) a large nucleus into two unequal fragments plus a few neutrons. Using this model, consider the case of a uranium nucleus fissioning into two spherical fragments, one with a charge e and radius m, the other with e and m. Calculate the electric potential energy (MeV) of these fragments, assuming that the charge is uniformly distributed throughout the volume of each spherical nucleus and that their surfaces are initially in contact at rest. The electrons surrounding the nuclei can be neglected. This electric potential energy will then be entirely converted to kinetic energy as the fragments repel each other. How does your predicted kinetic energy of the fragments agree with the observed value associated with uranium fission (approximately 200 MeV total)? [1 MeV = eV].
Question 2
The design of a magneto-optical atom trap requires a magnetic field that is directly proportional to position along an axis. Such a field perturbs the absorption of laser light by atoms in the manner needed to spatially confine atoms in the trap. Let us demonstrate that “anti-Helmholtz” coils will provide the required field , where is a constant. Anti-Helmholtz coils consist of two identical circular wire coils, each with radius and turns, carrying current in opposite directions. The coils share a common axis (defined as the axis with at the midpoint (0) between the coils). Assume that the centers of the coils are separated by a distance equal to the radius of the coils.
(a) Show that the magnetic field at position along the axis is given by
(b)For small excursions from the origin where , show that the magnetic field is given by , where the constant .
(c) For optimal atom trapping, should be about 0.15 T/m. Assume an atom trap uses anti-Helmholtz coils with = 4.0 cm and = 150. What current should flow through the coils? [Coil separation equal to coil radius, as assumed in this problem, is not a strict requirement for anti-Helmholtz coils.]















![{\displaystyle B(x)={\frac {4\mu _{0}NI}{R}}\left\{\left[4+\left(1-{\frac {2x}{R}}\right)^{2}\right]^{-{\frac {3}{2}}}-\left[4+\left(1+{\frac {2x}{R}}\right)^{2}\right]^{-{\frac {3}{2}}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67f6b5a240fd5dfa4244a3fd959be70a8312c119)



