Difference between revisions of "Chapter 4 Problem 67"
From 105/106 Lecture Notes by OBM
| Line 4: | Line 4: | ||
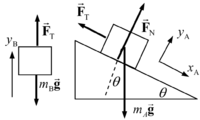
A block (mass <math>m_A</math>) lying on a fixed frictionless inclined plane is connected to a mass <math>m_B</math> by a cord passing over a pulley. | A block (mass <math>m_A</math>) lying on a fixed frictionless inclined plane is connected to a mass <math>m_B</math> by a cord passing over a pulley. | ||
| − | (a) Determine a formula for the acceleration of the system in terms of <math>m_A</math>, <math> | + | (a) Determine a formula for the acceleration of the system in terms of <math>m_A</math>, <math>m_B</math>, <math>\theta</math>, and <math>g</math>. |
| − | (b) What conditions apply to masses <math>m_A</math> and <math> | + | (b) What conditions apply to masses <math>m_A</math> and <math>m_B</math> for the acceleration to be in one direction (say, <math>m_A</math> down the plane), or in the opposite direction? Ignore the mass of the cord and pulley. |
==Solution== | ==Solution== | ||
Latest revision as of 10:30, 18 October 2019
Problem
A block (mass ) lying on a fixed frictionless inclined plane is connected to a mass by a cord passing over a pulley.
(a) Determine a formula for the acceleration of the system in terms of , , , and .
(b) What conditions apply to masses and for the acceleration to be in one direction (say, down the plane), or in the opposite direction? Ignore the mass of the cord and pulley.
Solution
Notice there are two coordinate systems A and B! However, the connection between them is trivial due to cord, and you save time in the end.
(a)
notice that in the chosen coordinate systems, and
The connection between the blocks mean
(b)
If the acceleration is down the plane, :
if the acceleration is up the plane