Chapter 25 Problem 93

Problem

The cross-section of a portion of a wire increases uniformly as shown, so it has the shape of a truncated cone. The diameter at one end is $a$ and at the other it is $b$, and the total length along the axis is $l$. If the material has resistivity $\rho$ determine the resistance $R$ between the two ends in terms of $a$, $b$, $l$, and $\rho$. Assume that the current flows uniformly through each section, and that the taper is small, i.e. $(b-a)\ll l$,

Solution

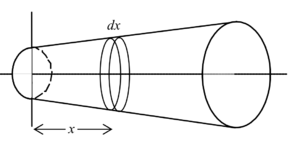
The total resistance is the combination of all the infinitesimal resistances due to the infinitesimal rings shown above. The current is aligned with the $x$ direction and the "length of the infinitesimal ring wire" is $dx$. The diameter of each slice is $a+{\frac {x}{l}}(b-a)$

$dR=\rho {\frac {dx}{\pi {\frac {1}{4}}\left(a+{\frac {x}{l}}(b-a)\right)^{2}}}\rightarrow$

$R=\int dR=\int _{0}^{l}\rho {\frac {dx}{\pi {\frac {1}{4}}\left(a+{\frac {x}{l}}(b-a)\right)^{2}}}$ $=-\left.{\frac {4\rho }{\pi }}{\frac {l}{b-a}}{\frac {1}{\left(a+{\frac {x}{l}}(b-a)\right)}}\right|_{0}^{l}$

  $={\frac {4\rho l}{\pi ab}}$