Difference between revisions of "Chapter 25 Problem 93"
From 105/106 Lecture Notes by OBM
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
==Problem== | ==Problem== | ||
| + | |||
[[File:Chapter_25_Problem_93_q.png|300px|center|The resistor]] | [[File:Chapter_25_Problem_93_q.png|300px|center|The resistor]] | ||
| + | |||
The cross-section of a portion of a wire increases uniformly as shown, so it has the shape of a truncated cone. The diameter at one end is <math>a</math> and at the other it is <math>b</math>, and the total length along the axis is <math>l</math>. If the material has resistivity <math>\rho</math> determine the resistance <math>R</math> between the two ends in terms of <math>a</math>, <math>b</math>, <math>l</math>, and <math>\rho</math>. Assume that the current flows uniformly through each section, and that the taper is small, i.e. <math>(b-a)\ll l</math>, | The cross-section of a portion of a wire increases uniformly as shown, so it has the shape of a truncated cone. The diameter at one end is <math>a</math> and at the other it is <math>b</math>, and the total length along the axis is <math>l</math>. If the material has resistivity <math>\rho</math> determine the resistance <math>R</math> between the two ends in terms of <math>a</math>, <math>b</math>, <math>l</math>, and <math>\rho</math>. Assume that the current flows uniformly through each section, and that the taper is small, i.e. <math>(b-a)\ll l</math>, | ||
==Solution== | ==Solution== | ||
| − | [[File | + | |
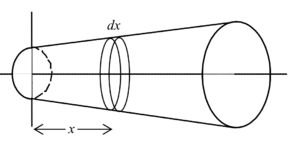
| + | [[File:Chapter25Problem93s.png|300px|center|The resistor in pieces]] | ||
The total resistance is the combination of all the infinitesimal resistances due to the infinitesimal rings shown above. The current is aligned with the <math>x</math> direction and the "length of the infinitesimal ring wire" is <math>dx</math>. The diameter of each slice is <math>a+\frac{x}{l}(b-a)</math> | The total resistance is the combination of all the infinitesimal resistances due to the infinitesimal rings shown above. The current is aligned with the <math>x</math> direction and the "length of the infinitesimal ring wire" is <math>dx</math>. The diameter of each slice is <math>a+\frac{x}{l}(b-a)</math> | ||
| Line 14: | Line 17: | ||
<math>=-\left.\frac{4\rho}{\pi}\frac{l}{b-a}\frac{1}{\left(a+\frac{x}{l}(b-a)\right)}\right|_0^l</math> | <math>=-\left.\frac{4\rho}{\pi}\frac{l}{b-a}\frac{1}{\left(a+\frac{x}{l}(b-a)\right)}\right|_0^l</math> | ||
| − | <math>\frac{4\rho l}{\pi a b}</math> | + | <math>=\frac{4\rho l}{\pi a b}</math> |
Latest revision as of 16:13, 6 April 2020
Problem
The cross-section of a portion of a wire increases uniformly as shown, so it has the shape of a truncated cone. The diameter at one end is and at the other it is , and the total length along the axis is . If the material has resistivity determine the resistance between the two ends in terms of , , , and . Assume that the current flows uniformly through each section, and that the taper is small, i.e. ,
Solution
The total resistance is the combination of all the infinitesimal resistances due to the infinitesimal rings shown above. The current is aligned with the direction and the "length of the infinitesimal ring wire" is . The diameter of each slice is