Chapter 26 Problem 68

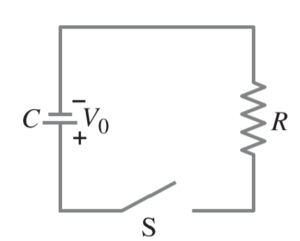
Problem

For the circuit shown, show that the decrease in energy stored in the capacitor from t = 0 until one time constant has elapsed equals the energy dissipated as heat in the resistor.

Solution

The energy stored in the capacitor is

$U={\frac {1}{2}}{\frac {Q^{2}}{C}}$

The power dissipated in the resistor is

$P=I^{2}R$

The charge on the capacitor and current in the resistor both decrease exponentially, with a time constant $\tau =RC$

$Q=Q_{0}e^{-t/RC}$; $I=I_{0}e^{-t/RC}={\frac {V_{0}}{R}}e^{-t/RC}={\frac {Q_{0}}{RC}}e^{-t/RC}$

$U_{\text{decrease}}=-\Delta U=U_{t=0}-U_{t=\tau }$ $={\frac {1}{2}}\left({\frac {Q^{2}}{C}}\right)_{t=0}-{\frac {1}{2}}\left({\frac {Q^{2}}{C}}\right)_{t=\tau }$ $={\frac {1}{2}}{\frac {Q_{0}^{2}}{C}}-{\frac {1}{2}}\left({\frac {Q_{0}e^{-1}}{C}}\right)^{2}$ $={\frac {1}{2}}{\frac {Q_{0}^{2}}{C}}\left(1-e^{-2}\right)$

$U_{\text{dissipated}}=\int Pdt=\int _{0}^{\tau }I^{2}Rdt=\int _{0}^{\tau }\left({\frac {Q_{0}}{RC}}e^{-t/RC}\right)^{2}Rdt$ ${\frac {Q_{0}^{2}}{RC^{2}}}\int _{0}^{\tau }e^{-2t/RC}dt={\frac {Q_{0}^{2}}{RC^{2}}}\left(-{\frac {RC}{2}}\right)\left(e^{-2t/RC}\right)_{0}^{\tau }$ $=-{\frac {1}{2}}{\frac {Q_{0}^{2}}{C}}\left(1-e^{-2}\right)$

$U_{\text{decrease}}=U_{\text{dissipated}}$