Difference between revisions of "Chapter 22 Problem 30"
From 105/106 Lecture Notes by OBM
| Line 17: | Line 17: | ||
<math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q</math> | <math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q</math> | ||
| − | <math>E_q=\frac{q}{4\pi\ | + | <math>E_q=\frac{q}{4 \pi \epsilon_0 r^2}</math> (radially pointing from the charge) |
| − | <math>E_\textrm{sphere}\rightarrow \oint \vec{E} \cdot d\vec{A}=E(4\pi | + | <math>E_\textrm{sphere}\rightarrow \oint \vec{E} \cdot d\vec{A}=E(4\pi r^2)=\frac{Q_\textrm{encl}}{\epsilon_0}</math> (radial direction) |
<math>E_\textrm{sphere}=\frac{Q_\textrm{encl}}{4\pi\epsilon_0 r^2}</math> | <math>E_\textrm{sphere}=\frac{Q_\textrm{encl}}{4\pi\epsilon_0 r^2}</math> | ||
so the question is about finding the <math>Q_\textrm{encl}</math> | so the question is about finding the <math>Q_\textrm{encl}</math> | ||
Revision as of 07:21, 21 March 2019
Problem
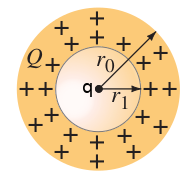
A nonconducting sphere has a spherical cavity of radius centered at the sphere’s center. Assuming the charge is distributed uniformly in the “shell” (between and ), determine the electric field as a function of for
(a)
(b)
(c)
Solution
Superposition principle
(radially pointing from the charge)
(radial direction)
so the question is about finding the