Difference between revisions of "Chapter 27 Problem 76"
(Created page with "==Problem== thumb|right|Magnetic seesaw A uniform conducting rod of length <math>d</math> and mass <math>m</math> sits atop a fulcrum, which i...") |
|||
| Line 4: | Line 4: | ||
==solution== | ==solution== | ||
| + | [[File:Chapter27problem76s.png|300px|center|The magnetic seesaw]] | ||
| + | |||
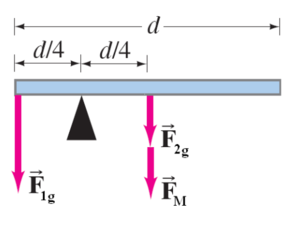
| + | Since the magnetic and gravitational force along the entire rod is uniform, the two forces can be considered to be acting at the center of mass of the rod. To be balanced, the net torque about the fulcrum must be zero. Using the usual sign convention for torques: | ||
| + | |||
| + | <math>\sum\tau=0</math> | ||
| + | |||
| + | <math>\sum\tau=Mg\left(\frac{1}{4}d\right)-mg\left(\frac{1}{4}d\right)-F_M\left(\frac{1}{4}d\right)</math> | ||
| + | |||
| + | <math>F_M=(M-m)g</math> | ||
| + | |||
| + | <math>I=\frac{F}{lB}=\frac{(M-m)g}{dB}=\frac{F}{lB}=\frac{7mg}{dB}</math> | ||
Latest revision as of 04:45, 9 April 2019
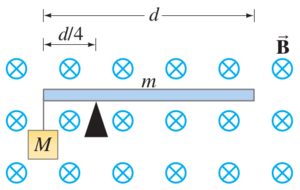
Problem
A uniform conducting rod of length and mass sits atop a fulcrum, which is placed a distance from the rod’s left-hand end and is immersed in a uniform magnetic field of magnitude directed into the page. An object whose mass is 8.0 times greater than the rod’s mass is hung from the rod’s left-hand end. What current (direction and magnitude) should flow through the rod in order for it to be “balanced” (i.e., be at rest horizontally) on the fulcrum? (Flexible connecting wires which exert negligible force on the rod are not shown.)
solution
Since the magnetic and gravitational force along the entire rod is uniform, the two forces can be considered to be acting at the center of mass of the rod. To be balanced, the net torque about the fulcrum must be zero. Using the usual sign convention for torques: