Difference between revisions of "Solutions 060519"
From 105/106 Lecture Notes by OBM
| Line 13: | Line 13: | ||
Set <math>x = 0 </math> at the midpoint on the axis between the two loops. Since the loops are a distance <math>R</math> apart, the center of one loop will be at <math>x =-\frac{1}{2} R</math> and the center of the other at <math>x =+\frac{1}{2} R</math> . The currents in the loops flow in opposite directions, so by the right-hand-rule the magnetic fields from the two wires will subtract from each other. | Set <math>x = 0 </math> at the midpoint on the axis between the two loops. Since the loops are a distance <math>R</math> apart, the center of one loop will be at <math>x =-\frac{1}{2} R</math> and the center of the other at <math>x =+\frac{1}{2} R</math> . The currents in the loops flow in opposite directions, so by the right-hand-rule the magnetic fields from the two wires will subtract from each other. | ||
| + | |||
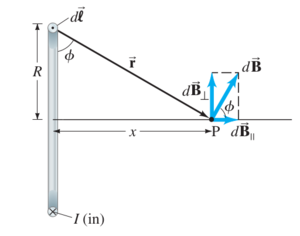
| + | for the single coil: | ||
| + | |||
[[File:Exercise060519Problem2s1.png|300px|center|Field due to a coil]] | [[File:Exercise060519Problem2s1.png|300px|center|Field due to a coil]] | ||
| Line 18: | Line 21: | ||
<math>B=B_\parallel=\int dB \cos \phi =\int dB \frac{R}{r}=\int dB \frac{R}{(R^2+x^2)^{\frac{1}{2}}}=\frac{\mu_0 I}{4\pi r^2}\frac{R}{(R^2+x^2)^{\frac{1}{2}}}\int dl = \frac{\mu_0 I R^2}{2(R^2+x^2)^{\frac{3}{2}}}</math> | <math>B=B_\parallel=\int dB \cos \phi =\int dB \frac{R}{r}=\int dB \frac{R}{(R^2+x^2)^{\frac{1}{2}}}=\frac{\mu_0 I}{4\pi r^2}\frac{R}{(R^2+x^2)^{\frac{1}{2}}}\int dl = \frac{\mu_0 I R^2}{2(R^2+x^2)^{\frac{3}{2}}}</math> | ||
| + | |||
| + | In the anti-helmholtz setup: | ||
| + | |||
| + | <math>B(x)=\frac{\mu_0 NI R^2}{2\left[R^2+\left(\frac{1}{2}R-x\right)^2\right]^{\frac{3}{2}}}-\frac{\mu_0 NI R^2}{2\left[R^2+\left(\frac{1}{2}R+x\right)^2\right]^{\frac{3}{2}}}</math> | ||
| + | |||
| + | <math>B(x)=\frac{\mu_0 NI }{R\left[4+\left(1-2x/R\right)^2\right]^{\frac{3}{2}}}-\frac{\mu_0 NI }{R\left[4+\left(1+2x/R\right)^2\right]^{\frac{3}{2}}}</math> | ||
| + | |||
| + | <math>)=\frac{4\mu_0 NI}{R}\left\{\left[4+\left(1-\frac{2x}{R}\right)^2\right]^{-\frac{3}{2}}-\left[4+\left(1+\frac{2x}{R}\right)^2\right]^{-\frac{3}{2}}\right\}</math> | ||
Revision as of 06:37, 6 May 2019
Question 1
The two fragments can be treated as point charges for purposes of calculating their potential energy. Using energy conservation, the potential energy is all converted to kinetic energy as the two fragments separate to a large distance.
This is about %25 greater than the observed kinetic energy of 200 MeV
Question 2
(a)
Set at the midpoint on the axis between the two loops. Since the loops are a distance apart, the center of one loop will be at and the center of the other at . The currents in the loops flow in opposite directions, so by the right-hand-rule the magnetic fields from the two wires will subtract from each other.
for the single coil:
In the anti-helmholtz setup:








![{\displaystyle B(x)={\frac {\mu _{0}NIR^{2}}{2\left[R^{2}+\left({\frac {1}{2}}R-x\right)^{2}\right]^{\frac {3}{2}}}}-{\frac {\mu _{0}NIR^{2}}{2\left[R^{2}+\left({\frac {1}{2}}R+x\right)^{2}\right]^{\frac {3}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/991a4b70162a6390c0d1ec74dfe74c6ce5e5a953)
![{\displaystyle B(x)={\frac {\mu _{0}NI}{R\left[4+\left(1-2x/R\right)^{2}\right]^{\frac {3}{2}}}}-{\frac {\mu _{0}NI}{R\left[4+\left(1+2x/R\right)^{2}\right]^{\frac {3}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bc89e2846143c18d0b14a5bad7f5fddbf0f923e)
![{\displaystyle )={\frac {4\mu _{0}NI}{R}}\left\{\left[4+\left(1-{\frac {2x}{R}}\right)^{2}\right]^{-{\frac {3}{2}}}-\left[4+\left(1+{\frac {2x}{R}}\right)^{2}\right]^{-{\frac {3}{2}}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aebacc3b11e9af534484177ba189d024dede6012)