Difference between revisions of "Exercise 070519"
From 105/106 Lecture Notes by OBM
| Line 18: | Line 18: | ||
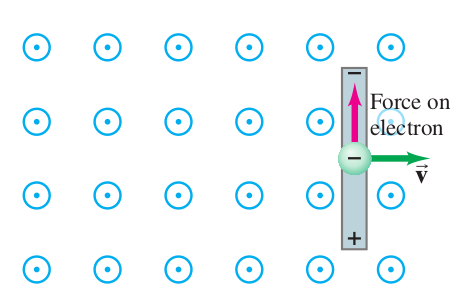
<math>\mathcal{E}=V_{\textrm{up}}-V_{\textrm{down}}=El=vBl</math> | <math>\mathcal{E}=V_{\textrm{up}}-V_{\textrm{down}}=El=vBl</math> | ||
| − | [[File:Exercise070519Problem1q2.png| | + | [[File:Exercise070519Problem1q2.png|400px|center|Wire and magnetic field]] |
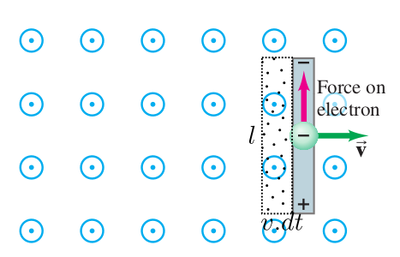
The flux cut by conductor in time <math>dt</math> is | The flux cut by conductor in time <math>dt</math> is | ||
Revision as of 08:24, 7 May 2019
Problem 1
Derive the induced emf between the ends of a metallic rod of length moving at a constant velocity in a uniform magnetic field using Lorentz force. Verify your result with the Faraday's law of induction.
Solution
The metallic rod can be thought as a container for electrons. As the rod moves in the magnetic field, the electrons also move in the electric field with the same velocity. Thus they experience a force . As the electrons move, they leave a region in the rod which is charge depleted. This creates an electric field. In the steady state, the force due to electric field balances the force due to magnetic field
The flux cut by conductor in time is
The magnitude of the emf induced is then