Difference between revisions of "Chapter 3 Problem 64"
From 105/106 Lecture Notes by OBM
(Created page with "__NOTOC__ ==Problem== An airplane is heading due south at a speed of 580 km/h. If a wind begins blowing from the southwest at a speed of 90.0 km/h (average), calculate (a) t...") |
(→(b)) |
||
| Line 25: | Line 25: | ||
The wind speed is 90.0 km/h, so after 11.0 min the plane is off course by: | The wind speed is 90.0 km/h, so after 11.0 min the plane is off course by: | ||
| − | <math>\Delta x=v_x t=\left(90\textrm{km/h}\right)\left(11\textrm{min}\right)\left(\frac{1\textrm{h}} | + | <math>\Delta x=v_x t=\left(90\textrm{km/h}\right)\left(11\textrm{min}\right)\left(\frac{1\textrm{h}}{60\textrm{min}}\right)=16.5\textrm{km}</math> |
Latest revision as of 22:06, 8 October 2019
Problem
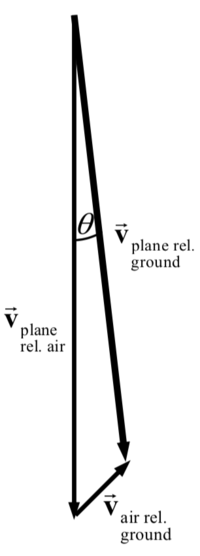
An airplane is heading due south at a speed of 580 km/h. If a wind begins blowing from the southwest at a speed of 90.0 km/h (average), calculate
(a) the velocity (magnitude and direction) of the plane, relative to the ground, and
(b) how far from its intended position it will be after 11.0 min if the pilot takes no corrective action.
[Hint: First draw a diagram.]
Solution
(a)
(7 degrees east of south)
(b)
The wind speed is 90.0 km/h, so after 11.0 min the plane is off course by: