Difference between revisions of "Chapter 9 Problem 89"
From 105/106 Lecture Notes by OBM
(Created page with "__NOTOC__ ==Problem== 250px|right|diagram A gun fires a bullet vertically into a 1.40-kg block of wood at rest on a thin horizontal sheet. If t...") |
|||
| Line 6: | Line 6: | ||
The collision is totally inelastic and conserves momentum. In the second part the energy is conserved in the rising of the block and embedded bullet after the collision. | The collision is totally inelastic and conserves momentum. In the second part the energy is conserved in the rising of the block and embedded bullet after the collision. | ||
| − | <math>v=\frac{m+M}{m}\sqrt{2gh}</math> | + | first part: |
| + | <math>P_i=P_f</math> | ||
| + | <math>\rightarrow mv=(m+M)v^\prime</math> | ||
| + | |||
| + | second part: | ||
| + | <math>K_i+U_i = K_f + U_f</math> | ||
| + | <math>\rightarrow \frac{1}{2}(m+M)v^{\prime 2}+0=0+(m+M)gh</math> | ||
| + | |||
| + | |||
| + | <math>v^\prime=\sqrt{2gh}</math> | ||
| + | |||
| + | hence | ||
| + | |||
| + | <math>v=\frac{m+M}{m}v^\prime=\frac{m+M}{m}\sqrt{2gh}</math> | ||
| + | |||
<math>\rightarrow h=\frac{1}{2g}\left(\frac{mv}{m+M}\right)^2=\frac{1}{2\left(9.80 \text{m/s}^2\right)}\left(\frac{\left(0.0240\text{kg}\right)\left(310\text{m/s}\right)}{\left(0.0240\text{kg}\right)+\left(1.40\text{kg}\right)}\right)^2 = 1.4 \text{m}</math> | <math>\rightarrow h=\frac{1}{2g}\left(\frac{mv}{m+M}\right)^2=\frac{1}{2\left(9.80 \text{m/s}^2\right)}\left(\frac{\left(0.0240\text{kg}\right)\left(310\text{m/s}\right)}{\left(0.0240\text{kg}\right)+\left(1.40\text{kg}\right)}\right)^2 = 1.4 \text{m}</math> | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<math></math> | <math></math> | ||
Latest revision as of 16:58, 25 November 2019
Problem
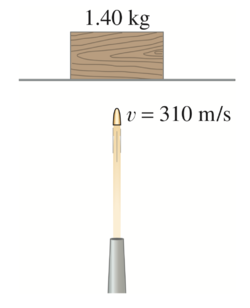
A gun fires a bullet vertically into a 1.40-kg block of wood at rest on a thin horizontal sheet. If the bullet has a mass of 24.0 g and a speed of 310 m/s, how high will the block rise into the air after the bullet becomes embedded in it?
Solution
The collision is totally inelastic and conserves momentum. In the second part the energy is conserved in the rising of the block and embedded bullet after the collision.
first part:
second part:
hence