Difference between revisions of "Chapter 26 Problem 68"
From 105/106 Lecture Notes by OBM
(Created page with "__NOTOC__ ==Problem== 300px|center|loops For the circuit shown, show that the decrease in energy stored in the capacitor from t = 0 until one...") |
|||
| Line 21: | Line 21: | ||
<math>=\frac{1}{2}\frac{Q_0^2}{C}-\frac{1}{2}\left(\frac{Q_0e^{-1}}{C}\right)^2</math> | <math>=\frac{1}{2}\frac{Q_0^2}{C}-\frac{1}{2}\left(\frac{Q_0e^{-1}}{C}\right)^2</math> | ||
<math>=\frac{1}{2}\frac{Q_0^2}{C}\left(1-e^{-2}\right)</math> | <math>=\frac{1}{2}\frac{Q_0^2}{C}\left(1-e^{-2}\right)</math> | ||
| + | |||
| + | <math>U_\text{dissipated}=\int P dt=\int_0^\tau I^2 R dt=\int_0^\tau\left(\frac{Q_0}{RC}e^{-t/RC}\right)^2 R dt</math> | ||
| + | <math>\frac{Q^2_0}{RC^2}\int_0^\tau e^{-2t/RC}dt=\frac{Q_0^2}{RC^2}\left(\right)</math> | ||
Revision as of 14:53, 17 April 2020
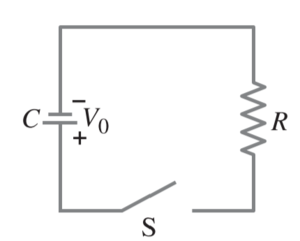
Problem
For the circuit shown, show that the decrease in energy stored in the capacitor from t = 0 until one time constant has elapsed equals the energy dissipated as heat in the resistor.
Solution
The energy stored in the capacitor is
The power dissipated in the resistor is
The charge on the capacitor and current in the resistor both decrease exponentially, with a time constant
;