Difference between revisions of "Chapter 22 Problem 30"
From 105/106 Lecture Notes by OBM
| Line 13: | Line 13: | ||
==Solution== | ==Solution== | ||
| + | Superposition principle | ||
| + | |||
| + | <math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q</math> | ||
| + | |||
| + | <math>E_q=\frac{q}{4\pi\epsilon_0r^2}<math> (radially pointing from the charge) | ||
| + | |||
| + | <math>E_\textrm{sphere}\rightarrow \oint \vec{E} \cdot d\vec{A}=E(4\pi\r^2)=\frac{Q_\textrm{encl}}{\epsilon_0}</math> (radial direction) | ||
| + | |||
| + | <math>E_\textrm{sphere}=\frac{Q_\textrm{encl}}{4\pi\epsilon_0 r^2}</math> | ||
| + | |||
| + | so the question is about finding the <math>Q_\textrm{encl}</math> | ||
Revision as of 07:19, 21 March 2019
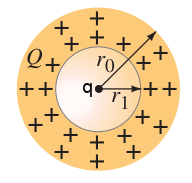
Problem
A nonconducting sphere has a spherical cavity of radius centered at the sphere’s center. Assuming the charge is distributed uniformly in the “shell” (between and ), determine the electric field as a function of for
(a)
(b)
(c)
Solution
Superposition principle
Failed to parse (unknown function "\r"): {\displaystyle E_q=\frac{q}{4\pi\epsilon_0r^2}<math> (radially pointing from the charge) <math>E_\textrm{sphere}\rightarrow \oint \vec{E} \cdot d\vec{A}=E(4\pi\r^2)=\frac{Q_\textrm{encl}}{\epsilon_0}} (radial direction)
so the question is about finding the