|
|
| Line 21: |
Line 21: |
| | | | |
| | ===(b)=== | | ===(b)=== |
| − | <math>R=\frac{(15 \times 10^{-5}\Omega\cdot \textrm{m}}{2\pi(0.024 \textrm{m})}\ln\left(\frac{1.8\textrm{mm}}{1.0\textrm{mm}}\right)=5.8\times10^{-4}\Omega</math> | + | <math>R=\frac{15 \times 10^{-5}\Omega\cdot \textrm{m}}{2\pi(0.024 \textrm{m})}\ln\left(\frac{1.8\textrm{mm}}{1.0\textrm{mm}}\right)=5.8\times10^{-4}\Omega</math> |
| | | | |
| | ===(c)=== | | ===(c)=== |
| | | | |
| − | <math>R=\frac{\rho l}{A}=\frac{\rho l}{\pi (r_2^2-r_1^2)}=\frac{(15 \times 10^{-5}\Omega\cdot \textrm{m}(0.024 \textrm{m}))}{\pi\left[(1.8\times10^{-3}\textrm{m})^2-(1.0\times10^{-3}\textrm{m})^2\right]}=0.51\Omega</math> | + | <math>R=\frac{\rho l}{A}=\frac{\rho l}{\pi (r_2^2-r_1^2)}=\frac{(15 \times 10^{-5}\Omega\cdot \textrm{m})(0.024 \textrm{m})}{\pi\left[(1.8\times10^{-3}\textrm{m})^2-(1.0\times10^{-3}\textrm{m})^2\right]}=0.51\Omega</math> |
Revision as of 04:00, 25 March 2019
Problem
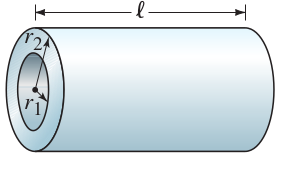
A hollow cylindrical resistor with inner radius  and outer radius
and outer radius  , and length
, and length  , is made of a material whose resistivity is
, is made of a material whose resistivity is 
(a) Show that the resistance is given by

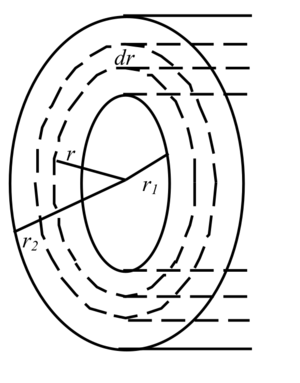
for current that flows radially outward. [Hint: Divide the resistor into concentric cylindrical shells and integrate.]
(b) Evaluate the resistance  for such a resistor made of carbon whose inner and outer radii are 1.0 mm and 1.8 mm and whose length is 2.4 cm (Choose
for such a resistor made of carbon whose inner and outer radii are 1.0 mm and 1.8 mm and whose length is 2.4 cm (Choose  .)
.)
(c) What is the resistance in part (b) for current flowing parallel to the axis?
Solution
(a)


(b)

(c)
![{\displaystyle R={\frac {\rho l}{A}}={\frac {\rho l}{\pi (r_{2}^{2}-r_{1}^{2})}}={\frac {(15\times 10^{-5}\Omega \cdot {\textrm {m}})(0.024{\textrm {m}})}{\pi \left[(1.8\times 10^{-3}{\textrm {m}})^{2}-(1.0\times 10^{-3}{\textrm {m}})^{2}\right]}}=0.51\Omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/66dcdd7018daf982f83d0d1c03d67b3ba33d4e52)










![{\displaystyle R={\frac {\rho l}{A}}={\frac {\rho l}{\pi (r_{2}^{2}-r_{1}^{2})}}={\frac {(15\times 10^{-5}\Omega \cdot {\textrm {m}})(0.024{\textrm {m}})}{\pi \left[(1.8\times 10^{-3}{\textrm {m}})^{2}-(1.0\times 10^{-3}{\textrm {m}})^{2}\right]}}=0.51\Omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/66dcdd7018daf982f83d0d1c03d67b3ba33d4e52)