Chapter 26 Problem 40

Problem

Resistance is futile!

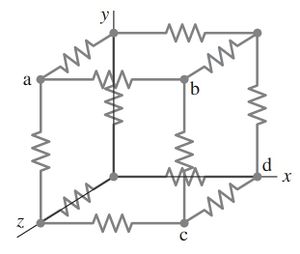
Twelve resistors, each of resistance R, are connected as the edges of a cube. Determine the equivalent resistance

(a) between points a and b, the ends of a side;

(b) between points a and c, the ends of a face diagonal;

(c) between points a and d, the ends of the volume diagonal.

[Hint: Apply an emf and determine currents; use symmetry at junctions.]

solution

(a)

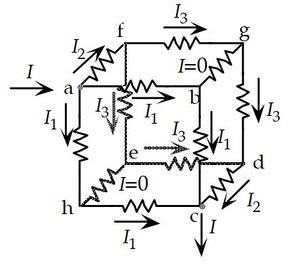
Insert a probe battery between points (a) and (b). Let's label the current drawn from this probe battery as I

This setup has a symmetry plane between abed, so the current split at junction a will be $I=I_{1}+I_{1}+I_{2}$

Another symmetry is that the afhe plane is the mirror cdgb (since one has the current I entering, and the other has the current leaving) thus we have the same currents in erverse directions in those planes.

The 6 equations in the symmetry reduced cube is:

1. $I=2I_{1}+I_{2}$
2. $I_{3}+I_{4}=I_{1}$
3. $I_{5}=2I_{4}$
4. $0=-2I_{1}R-I_{3}R+I_{2}R$
5. $0=-2I_{4}R-I_{5}R+I_{3}R$
6. $0={\mathcal {E}}-I_{2}R$

6 equations and 6 unknowns, so we start solving:

1. $I=2(I_{3}+I_{4})+{\frac {\mathcal {E}}{R}}$ (2 and 6 in 1)
2. $0=-2(I_{3}+I_{4})R-I_{3}R+{\frac {\mathcal {E}}{R}}R=-2I_{4}R-3I_{3}R+{\mathcal {E}}$ (2 and 6 in 4)
3. $0=-2I_{4}R-2I_{4}R+I_{3}R=-4I_{4}R+I_{3}R$ (3 in 5)

$I_{3}=4I_{4}$ ( solution of 3)

$0=-2I_{4}R-3(4I_{4})R+{\mathcal {E}}\rightarrow I_{4}={\frac {\mathcal {E}}{14R}}$ (previous into 2)

$I=2(4I_{4})+2(I_{4})+{\frac {\mathcal {E}}{R}}=10I_{4}+{\frac {\mathcal {E}}{R}}={\frac {10{\mathcal {E}}}{14R}}+{\frac {\mathcal {E}}{R}}={\frac {12{\mathcal {E}}}{7R}}$ (previous into 1)

$R_{\textrm {eq}}={\frac {\mathcal {E}}{I}}={\frac {7}{12}}R$

(b)

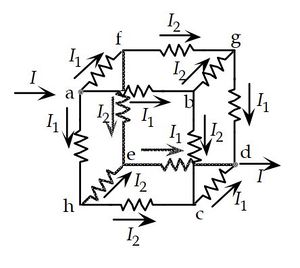
Insert a probe battery between points (a) and (c). Let's label the current drawn from this probe battery as I

(c)

Insert a probe battery between points (a) and (d). Let's label the current drawn from this probe battery as I