Chapter 28 Problem 24

Problem

Current loop and wire

A triangular loop of side length a carries a current $I$. If this loop is placed a distance $d$ away from a very long straight wire carrying a current $I^{\prime }$,determine the force on the loop.

Solution

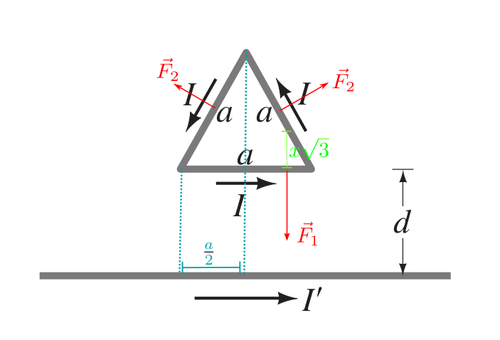
The current in the parallel branch flows in the same direction as the long straight wire, so the force is attractive with magnitude:

$F_{1}={\frac {\mu _{0}II^{\prime }}{2\pi d}}a$

By symmetry the magnetic force for the other two segments will be equal.

$F_{2y}=\int _{0}^{a/2}{\frac {\mu _{0}II^{\prime }}{2\pi \left(d+{\sqrt {3}}x\right)}}dx={\frac {\mu _{0}II^{\prime }}{2\pi {\sqrt {3}}}}\left.\ln \left(d+{\sqrt {3}}x\right)\right|_{0}^{a/2}$ $={\frac {\mu _{0}II^{\prime }}{2\pi {\sqrt {3}}}}\ln \left(1+{\frac {{\sqrt {3}}a}{2d}}\right)$

The magnitude of the net force is:

$F_{1}-2F_{2y}={\frac {\mu _{0}II^{\prime }}{\pi }}\left[{\frac {a}{2d}}-{\frac {\sqrt {3}}{3}}\ln \left(1+{\frac {{\sqrt {3}}a}{2d}}\right)\right]$