Difference between revisions of "Chapter 29 Problem 35"
From 105/106 Lecture Notes by OBM
| Line 6: | Line 6: | ||
(b) in the opposite direction to <math>I</math>. | (b) in the opposite direction to <math>I</math>. | ||
| + | |||
| + | ==Solution== | ||
| + | [[File:Chapter29Problem35s.png|300px|center|Wire and current induced magnetic field]] | ||
| + | |||
| + | The magnetic field is perpendicular to the rod, with the magnetic field decreasing with distance from the rod. | ||
| + | |||
| + | ===(a)=== | ||
| + | <math>d\mathcal{E}=Bvdr</math> | ||
| + | |||
| + | <math>B=\frac{\mu_0}{2\pi}\frac{I}{r}</math> (near a straight long wire) | ||
| + | |||
| + | <math>\mathcal{E}=\int d\mathcal{E}=\int_b^{b+a}\frac{\mu_0 I}{2\pi r}v dr=\frac{\mu_0 Iv}{2\pi }\ln\left(\frac{b+a}{b}\right)</math> | ||
| + | |||
| + | The force is towards the long wire | ||
| + | |||
| + | ===(b)=== | ||
| + | same magnitude, away from the long wire | ||
Revision as of 07:33, 30 April 2019
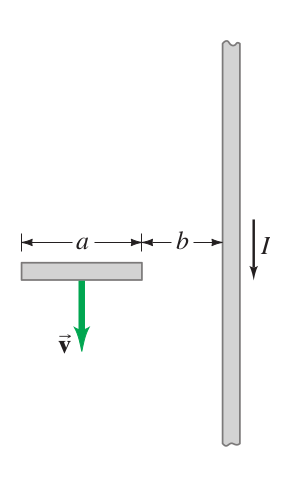
Problem
A short section of wire, of length , is moving with velocity , parallel to a very long wire carrying a current . The near end of the wire section is a distance from the long wire. Assuming the vertical wire is very long compared to , determine the emf between the ends of the short section. Assume is
(a) in the same direction as ,
(b) in the opposite direction to .
Solution
The magnetic field is perpendicular to the rod, with the magnetic field decreasing with distance from the rod.
(a)
(near a straight long wire)
The force is towards the long wire
(b)
same magnitude, away from the long wire