Exercise 070519

Problem 1

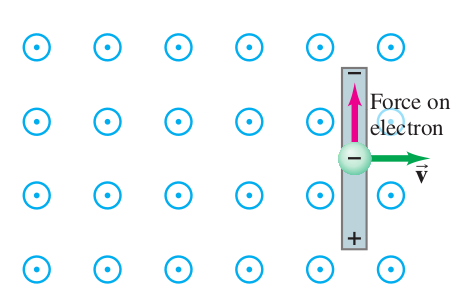
Derive the induced emf ${\mathcal {E}}$ between the ends of a metallic rod of length $l$ moving at a constant velocity in a uniform magnetic field using Lorentz force. Verify your result with the Faraday's law of induction.

Solution

The metallic rod can be thought as a container for electrons. As the rod moves in the magnetic field, the electrons also move in the electric field with the same velocity. Thus they experience a force ${\vec {F}}_{B}=-e{\vec {v}}\times {\vec {B}}$. As the electrons move, they leave a region in the rod which is charge depleted. This creates an electric field. In the steady state, the force due to electric field ${\vec {F}}_{E}=-e{\vec {E}}$ balances the force due to magnetic field

${\vec {F}}_{B}={\vec {F}}_{E}$

$-e\left|{\vec {v}}\times {\vec {B}}\right|=-evB=-e\left|{\vec {E}}\right|=-eE$

$E=vB$

${\mathcal {E}}=V_{\textrm {up}}-V_{\textrm {down}}=El=vBl$

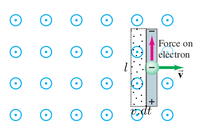
The flux cut by conductor in time $dt$ is

$d\Phi =B.ds=B.(lvdt)$

The magnitude of the emf induced is then

${\mathcal {E}}=\left|{\frac {d\Phi }{dt}}\right|=Bvl$