|
|
| Line 45: |
Line 45: |
| | The distance between the two spheres in small angle approximation is | | The distance between the two spheres in small angle approximation is |
| | | | |
| − | <math>d=l\sin\theta_1+l\sin\theta_2\approx(\theta_1+\theta_2)</math> | + | <math>d=l\sin\theta_1+l\sin\theta_2\approx l(\theta_1+\theta_2)</math> |
| | | | |
| | in the first case <math>\theta_1=\theta_2</math> thus: | | in the first case <math>\theta_1=\theta_2</math> thus: |
| Line 61: |
Line 61: |
| | <math>m_1g\theta_1=F_{E1}=\frac{kQ(2Q)}{d^2}=mg\frac{2d}{3l}</math> | | <math>m_1g\theta_1=F_{E1}=\frac{kQ(2Q)}{d^2}=mg\frac{2d}{3l}</math> |
| | | | |
| − | <math>d=\left( \frac{3lkQ^2}{mg}\right)</math> | + | <math>d=\left( \frac{3lkQ^2}{mg}\right)^{1/3}</math> |
| | | | |
| | <math></math> | | <math></math> |
Latest revision as of 22:12, 16 February 2020
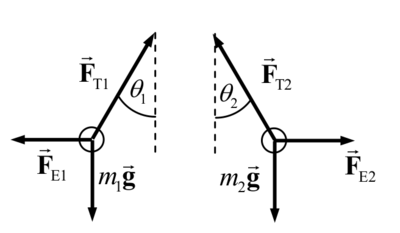
Problem
Two small charged spheres hang from cords of equal length  and make small angles
and make small angles  and
and  with the vertical.
with the vertical.
(a) If  ,
,  and
and  determine the ratio
determine the ratio 
(b) If  ,
,  and
and 
 determine the ratio
determine the ratio 
(c) Estimate the distance between the spheres for each case.
Solution
In the small angle approximation:
- the spheres only have horizontal displacement, and so the electric force of repulsion is always horizontal.

Since the spheres are in equilibrium, the net force in each direction is zero.
(a)


similarly

Apply Newton's third law:

Thus the answer is 1
(b)

(c)
The distance between the two spheres in small angle approximation is

in the first case  thus:
thus:



in the second case  thus:
thus: