Difference between revisions of "Chapter 21 Problem 67"
From 105/106 Lecture Notes by OBM
(Created page with "__NOTOC__ ==Problem== 200px|center|diagram (a) Show that at points along the axis of a dipole (along the same line that contains and ), the e...") |
|||
| Line 3: | Line 3: | ||
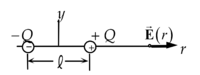
[[File:Chapter21Problem67q.png|200px|center|diagram]] | [[File:Chapter21Problem67q.png|200px|center|diagram]] | ||
| − | (a) Show that at points along the axis of a dipole (along the same line that contains and ), the electric field has magnitude | + | (a) Show that at points along the axis of a dipole (along the same line that contains <math>-Q</math> and <math>+Q</math>), the electric field has magnitude |
| − | + | <math>E=\frac{1}{4\pi\epsilon_0}\frac{2p}{r^3}</math> | |
| − | (b) In what direction does point? | + | for <math>r \gg l</math>, where <math>r</math> is the distance from a point to the center of the dipole. |
| + | |||
| + | (b) In what direction does <math>\vec{E}</math> point? | ||
==Solution== | ==Solution== | ||
| + | [[File:Chapter21Problem67s.png|200px|center|diagram]] | ||
| + | |||
| + | |||
| + | <math>E_\text{net}=E_\text{+Q}+E_\text{-Q}=\frac{Q}{4\pi\epsilon_0 \left(r-\frac{1}{2}l\right)^2}+\frac{(-Q)}{4\pi\epsilon_0 \left(r-\frac{1}{2}l\right)^2}</math> | ||
| + | <math></math> | ||
| + | <math></math> | ||
| + | <math></math> | ||
| + | <math></math> | ||
| + | <math></math> | ||
Revision as of 22:52, 16 February 2020
Problem
(a) Show that at points along the axis of a dipole (along the same line that contains and ), the electric field has magnitude
for , where is the distance from a point to the center of the dipole.
(b) In what direction does point?
Solution
