Chapter 21 Problem 67

Problem

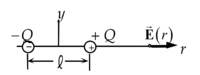
(a) Show that at points along the axis of a dipole (along the same line that contains $-Q$ and $+Q$), the electric field has magnitude

$E={\frac {1}{4\pi \epsilon _{0}}}{\frac {2p}{r^{3}}}$

for $r\gg l$, where $r$ is the distance from a point to the center of the dipole.

(b) In what direction does ${\vec {E}}$ point?

Solution

(a)

$E_{\text{net}}=E_{\text{+Q}}+E_{\text{-Q}}={\frac {Q}{4\pi \epsilon _{0}\left(r-{\frac {1}{2}}l\right)^{2}}}+{\frac {(-Q)}{4\pi \epsilon _{0}\left(r+{\frac {1}{2}}l\right)^{2}}}$ $={\frac {Q\left[\left(r+{\frac {1}{2}}l\right)^{2}-\left(r-{\frac {1}{2}}l\right)^{2}\right]}{4\pi \epsilon _{0}\left(r+{\frac {1}{2}}l\right)^{2}\left(r-{\frac {1}{2}}l\right)^{2}}}$ $={\frac {Q(2rl)}{4\pi \epsilon _{0}\left(r+{\frac {1}{2}}l\right)^{2}\left(r-{\frac {1}{2}}l\right)^{2}}}$ $\approx {\frac {Q(2rl)}{4\pi \epsilon _{0}r^{4}}}$ $={\frac {2Ql}{4\pi \epsilon _{0}r^{3}}}$ $={\frac {2p}{4\pi \epsilon _{0}r^{3}}}$

(The same result for the other side)

(b)

The electric field points in the same direction as the electric dipole moment vector.