Difference between revisions of "Chapter 21 Problem 86"
From 105/106 Lecture Notes by OBM
(Created page with "==Problem== thumb|right|line charge and orbiting electron An electron moves in a circle of radius <math>r</math> around a very long uniformly...") |
|||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
==Problem== | ==Problem== | ||
| − | [[File:Chapter21-problem86q.png| | + | [[File:Chapter21-problem86q.png|200px|right|line charge and orbiting electron]] |
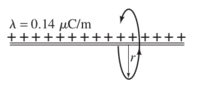
An electron moves in a circle of radius <math>r</math> around a very long uniformly charged wire in a vacuum chamber. The charge density on the wire is <math>\lambda = 0.14 \mu\textrm{C}/\textrm{m}</math>. | An electron moves in a circle of radius <math>r</math> around a very long uniformly charged wire in a vacuum chamber. The charge density on the wire is <math>\lambda = 0.14 \mu\textrm{C}/\textrm{m}</math>. | ||
| Line 9: | Line 10: | ||
==solution== | ==solution== | ||
===(a)=== | ===(a)=== | ||
| + | Has been done in the lecture. | ||
| + | |||
<math>E=\frac{1}{2\pi\epsilon_0}\frac{\lambda}{r}</math> which is radially away from the wire at all points. | <math>E=\frac{1}{2\pi\epsilon_0}\frac{\lambda}{r}</math> which is radially away from the wire at all points. | ||
===(b)=== | ===(b)=== | ||
| + | The force on the electron will point radially in, producing a centripetal acceleration. | ||
| + | |||
<math>\left|\vec{F}\right|=\left|q\vec{E}\right|=\frac{e}{2\pi\epsilon_0}\frac{\lambda}{r}</math> | <math>\left|\vec{F}\right|=\left|q\vec{E}\right|=\frac{e}{2\pi\epsilon_0}\frac{\lambda}{r}</math> | ||
Revision as of 23:07, 16 February 2020
Problem
An electron moves in a circle of radius around a very long uniformly charged wire in a vacuum chamber. The charge density on the wire is .
(a) What is the electric field at the electron (magnitude and direction in terms of and )?
(b) What is the speed of the electron?
solution
(a)
Has been done in the lecture.
which is radially away from the wire at all points.
(b)
The force on the electron will point radially in, producing a centripetal acceleration.
Using the centripetal term (from last year)