Chapter 22 Problem 60

Problem

Interface effects

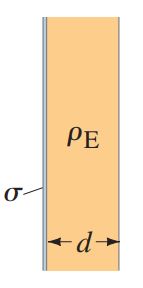
A very large thin plane has uniform surface charge density $\sigma$. Touching it on the right is a long wide slab of thickness d with uniform volume charge density $\rho _{E}$. Determine the electric field

(a) to the left of the plane,

(b) to the right of the slab, and

(c) everywhere inside the slab.

Solution

The field due to the plane is $E_{\textrm {plane}}={\frac {\sigma }{2\epsilon _{0}}}$ (as discussed in the lesson). Because the slab is very large, and we assume that we are considering only distances from the slab much less than its height or breadth, the symmetry of the slab results in its field being perpendicular to the slab, with a constant magnitude for a constant distance from its center. We also assume that $\rho _{E}>0$ and so the electric field of the slab points away from the center of the slab.

(a)

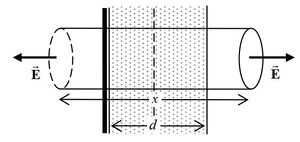
To the left of the plane, an easy choice is a cylindrical gaussian surface. There will be no flux through the curved wall of the cylinder. From the symmetry, the electric field is parallel to the surface area vector on both ends. Field due to the plane is the same on both ends, and by the symmetry of the problem and the field being independent of distance to the plane, the field due to the slab must also be the same on both ends. Thus the total field is the same magnitude on both ends.

$\oint {\vec {E}}\cdot d{\vec {A}}=\int _{\textrm {end}}{\vec {E}}\cdot d{\vec {A}}+\int _{\textrm {side}}{\vec {E}}\cdot d{\vec {A}}+\int _{\textrm {end}}{\vec {E}}\cdot d{\vec {A}}=\int _{\textrm {ends}}{\vec {E}}\cdot d{\vec {A}}+0={\frac {Q_{\textrm {encl}}}{\epsilon _{0}}}$

$2E_{\textrm {outside}}A={\frac {\sigma A+\rho _{E}dA}{\epsilon _{0}}}$

$E_{\textrm {outside}}=E_{\textrm {left}}={\frac {\sigma +\rho _{E}d}{2\epsilon _{0}}}$

(b)

due to symmetry (as discussed above)

$E_{\textrm {right}}=E_{\textrm {left}}={\frac {\sigma +\rho _{E}d}{2\epsilon _{0}}}$

(c)

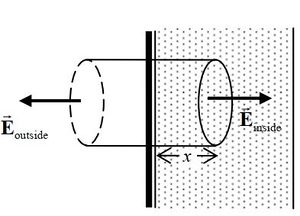
Inside the slab, we again exploit the same symmetry, but choose a gaussian surface that penetrates a distance x from the plane.

$\oint {\vec {E}}\cdot d{\vec {A}}=\int _{\textrm {left}}{\vec {E}}\cdot d{\vec {A}}+\int _{\textrm {side}}{\vec {E}}\cdot d{\vec {A}}+\int _{\textrm {right}}{\vec {E}}\cdot d{\vec {A}}=E_{\textrm {outside}}A+E_{\textrm {inside}}A+0={\frac {Q_{\textrm {encl}}}{\epsilon _{0}}}$

$Q_{\textrm {encl}}=\sigma A+\rho _{E}xA\rightarrow \left({\frac {\sigma +\rho _{E}d}{2\epsilon _{0}}}\right)A+E_{\textrm {inside}}A={\frac {\sigma A+\rho _{E}xA}{\epsilon _{0}}}$

$E_{\textrm {inside}}={\frac {\sigma +\rho _{E}(2x-d)}{2\epsilon _{0}}}$

Notice that at the right edge of the slab the field is continious, but at the left edge of the slab because of the surface charge density, field has a discontinuity.