|
|
| Line 49: |
Line 49: |
| | This is straightforward using Gauss's law and a surface that encompasses all the charges outside the shell | | This is straightforward using Gauss's law and a surface that encompasses all the charges outside the shell |
| | | | |
| − | <math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q=\frac{Q_\text{sphere}+1}{4\pi\epsilon_0 r^2}\hat{r}</math> | + | <math>\vec{E}_T=\vec{E}_\textrm{sphere}+\vec{E}_q=\frac{Q_\text{sphere}+q}{4\pi\epsilon_0 r^2}\hat{r}</math> |
Latest revision as of 09:39, 18 February 2020
Problem
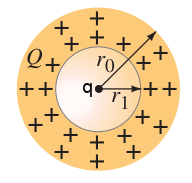
Non-conducting sphere with a charge inside
A nonconducting sphere has a spherical cavity of radius  centered at the sphere’s center. Assuming the charge
centered at the sphere’s center. Assuming the charge  is distributed uniformly in the “shell” (between
is distributed uniformly in the “shell” (between  and
and  ), determine the electric field as a function of
), determine the electric field as a function of  for
for
(a)

(b)

(c)

Solution
Superposition principle

 (radially pointing from the charge)
(radially pointing from the charge)
 (radial direction)
(radial direction)

so the question is about finding the 
(a)


(b)
First, let's calculate the uniform charge density  in terms of the charge held by the shell
in terms of the charge held by the shell  .
.


using this, we can calculate 
![{\displaystyle E_{\textrm {sphere}}={\frac {Q_{\textrm {encl}}}{4\pi \epsilon _{0}r^{2}}}={\frac {\rho \left[{\frac {4}{3}}\pi r^{3}-{\frac {4}{3}}\pi r_{1}^{3}\right]}{4\pi \epsilon _{0}r^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97278c8d467fb279677dde2b2805ffc741aaa8fc)

![{\displaystyle {\vec {E}}_{T}={\vec {E}}_{\textrm {sphere}}+{\vec {E}}_{q}={\frac {1}{4\pi \epsilon _{0}r^{2}}}\left[q+Q_{\textrm {sphere}}{\frac {r^{3}-r_{1}^{3}}{r_{0}^{3}-r_{1}^{3}}}\right]{\hat {r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d086cf2bc32ab96d0572b8cda435b070917a361)
(c)
This is straightforward using Gauss's law and a surface that encompasses all the charges outside the shell





















![{\displaystyle E_{\textrm {sphere}}={\frac {Q_{\textrm {encl}}}{4\pi \epsilon _{0}r^{2}}}={\frac {\rho \left[{\frac {4}{3}}\pi r^{3}-{\frac {4}{3}}\pi r_{1}^{3}\right]}{4\pi \epsilon _{0}r^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97278c8d467fb279677dde2b2805ffc741aaa8fc)

![{\displaystyle {\vec {E}}_{T}={\vec {E}}_{\textrm {sphere}}+{\vec {E}}_{q}={\frac {1}{4\pi \epsilon _{0}r^{2}}}\left[q+Q_{\textrm {sphere}}{\frac {r^{3}-r_{1}^{3}}{r_{0}^{3}-r_{1}^{3}}}\right]{\hat {r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d086cf2bc32ab96d0572b8cda435b070917a361)
