Difference between revisions of "Chapter 23 Problem 35"
From 105/106 Lecture Notes by OBM
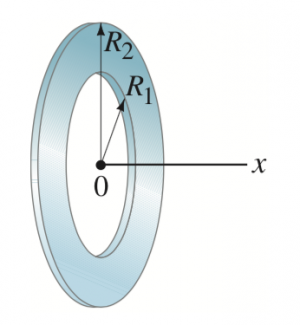
(Created page with "== Problem == thumb|right|The disc with a hole A flat ring of inner radius <math>R_1</math> and outer radius <math>R_2</math> carries a unifo...") |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | [[File:Chapter23_problem35q.png| | + | [[File:Chapter23_problem35q.png|center|300px|The disc with a hole]] |
A flat ring of inner radius <math>R_1</math> and outer radius <math>R_2</math> carries a uniform surface charge density <math>\sigma</math>. Determine the electric potential at points along the x axis | A flat ring of inner radius <math>R_1</math> and outer radius <math>R_2</math> carries a uniform surface charge density <math>\sigma</math>. Determine the electric potential at points along the x axis | ||
== Solution == | == Solution == | ||
| Line 9: | Line 9: | ||
<math>dq=\sigma dA=\sigma (2\pi R dR)</math> | <math>dq=\sigma dA=\sigma (2\pi R dR)</math> | ||
| − | <math>V=\frac{1}{4\pi\epsilon_0}\ | + | <math>V=\frac{1}{4\pi\epsilon_0}\int_{R_1}^{R_2}\frac{dq}{r}=\frac{1}{4\pi\epsilon_0}\int_{R_1}^{R_2}\frac{\sigma (2\pi R dR)}{\sqrt{x^2+R^2}}</math> |
| − | <math>=\frac{\sigma}{2\epsilon_0}\ | + | <math>=\frac{\sigma}{2\epsilon_0}\int_{R_1}^{R_2}\frac{R}{\sqrt{x^2+R^2}}dR</math> |
<math>x^2+R^2=u\rightarrow 2RdR=du\rightarrow RdR=\frac{1}{2}du</math> | <math>x^2+R^2=u\rightarrow 2RdR=du\rightarrow RdR=\frac{1}{2}du</math> | ||
Latest revision as of 22:29, 24 February 2020
Problem
A flat ring of inner radius and outer radius carries a uniform surface charge density . Determine the electric potential at points along the x axis
Solution
This is just a disc removed from the full disc we already solved in the chapter. Let's recycle things from there.
i.e. you just remove the inner hole's contribution from the total solution