Difference between revisions of "Chapter 24 Problem 63"
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
==Problem== | ==Problem== | ||
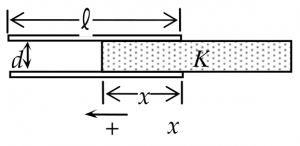
[[File:Chapter_24_problem_63.png|thumb|right|The capacitor with partial dielectric coverage]] | [[File:Chapter_24_problem_63.png|thumb|right|The capacitor with partial dielectric coverage]] | ||
Latest revision as of 18:14, 8 March 2020
Problem
- A slab of width d and dielectric constant K
- it is inserted a distance x into the space between the square parallel plates (of side l ) of a parallel plate capacitor
(a) the capacitance as a function of x
(b) the energy stored when is applied
(c) the magnitude and direction of the force exerted on the slab (assume is constant).
Solution
The first approximation would be to consider this as two connected parallel plate capacitors. Other effects can be added later (this is beyond the scope of this course). Since "high" and "low" plates are connected together, these are capacitors connected in parallel.
(a)
(b)
The capacitors are in parallel, so the potential difference between the plates is the same.
(c)
The (good) battery keeps the constant voltage and supplies charge to the capacitor as the dielectric is inserted. Since the dielectric slab is kept stationary, its kinetic energy is zero. All the change in energy in the battery-capacitor system is stored as potential energy.
The infinitesimal change in potential energy if we let the system go is
We can use this change in energy to calculate the tension force we need to supply.
Charge is conserved in this system so
Force is in direction, so to the right. Since this is a force keeping the slab from accelerating, the internal force acting on the system is
i.e. to the left. It means the induced charges on the slab are attracted by the plates.

![{\displaystyle C=C_{1}+C_{2}=\epsilon _{0}{\frac {l(l-x)}{d}}+K\epsilon _{0}{\frac {lx}{d}}=\epsilon _{0}{\frac {l^{2}}{d}}\left[1+(K-1){\frac {x}{l}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2db33e7faa719993fbe65f4a8693036d2a64a97)
![{\displaystyle U={\frac {1}{2}}(C_{1}+C_{2})V_{0}^{2}=\epsilon _{0}{\frac {l^{2}}{2d}}\left[1+(K-1){\frac {x}{l}}\right]V_{0}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e643cd106d646c09c73a428d35e1311cbeca11da)





![{\displaystyle =-{\frac {1}{2}}V_{0}^{2}\epsilon _{0}{\frac {l^{2}}{d}}\left[{\frac {(K-1)}{l}}\right]=-{\frac {V_{0}^{2}\epsilon _{0}l}{2d}}(K-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6ae1fbffeca8e68485b08b5254c53abddeade63)

