|
|
| Line 23: |
Line 23: |
| | | | |
| | <math>U_\text{dissipated}=\int P dt=\int_0^\tau I^2 R dt=\int_0^\tau\left(\frac{Q_0}{RC}e^{-t/RC}\right)^2 R dt</math> | | <math>U_\text{dissipated}=\int P dt=\int_0^\tau I^2 R dt=\int_0^\tau\left(\frac{Q_0}{RC}e^{-t/RC}\right)^2 R dt</math> |
| − | <math>\frac{Q^2_0}{RC^2}\int_0^\tau e^{-2t/RC}dt=\frac{Q_0^2}{RC^2}\left(\right)</math> | + | <math>\frac{Q^2_0}{RC^2}\int_0^\tau e^{-2t/RC}dt=\frac{Q_0^2}{RC^2}\left(-\frac{RC}{2}\right)\left(e^{-2t/RC}\right)_0^\tau</math> |
| | + | <math>=-\frac{1}{2}\frac{Q_0^2}{C}\left(1-e^{-2}\right)</math> |
| | + | |
| | + | <math>U_\text{decrease}=U_\text{dissipated}</math> |
Latest revision as of 14:58, 17 April 2020
Problem
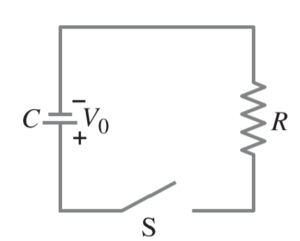
For the circuit shown, show that the decrease in energy stored in the capacitor from t = 0 until one time constant has elapsed equals the energy dissipated as heat in the resistor.
Solution
The energy stored in the capacitor is

The power dissipated in the resistor is

The charge on the capacitor and current in the resistor both decrease exponentially, with a time constant 
 ;
;