Chapter 22 Problem 30

Problem

Non-conducting sphere with a charge inside

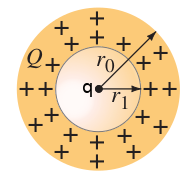
A nonconducting sphere has a spherical cavity of radius $r_{1}$ centered at the sphere’s center. Assuming the charge $Q$ is distributed uniformly in the “shell” (between $r=r_{1}$ and $r=r_{0}$ ), determine the electric field as a function of $r$ for

(a) $0<r<r_{1}$

(b) $r_{1}<r<r_{0}$

(c) $r>r_{0}$

Solution

Superposition principle

${\vec {E}}_{T}={\vec {E}}_{\textrm {sphere}}+{\vec {E}}_{q}$

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_q=\frac{q}{4\pi\epsilon_0r^2}<math> (radially pointing from the charge) <math>E_\textrm{sphere}\rightarrow \oint \vec{E} \cdot d\vec{A}=E(4\pi\r^2)=\frac{Q_\textrm{encl}}{\epsilon_0}} (radial direction)

$E_{\textrm {sphere}}={\frac {Q_{\textrm {encl}}}{4\pi \epsilon _{0}r^{2}}}$

so the question is about finding the $Q_{\textrm {encl}}$