SolPr1

Question1

We consider the cylinder as two cylindrical capacitors in parallel. The two “negative plates” are the (connected) halves of the inner cylinder (half of which is in contact with liquid, and half of which is in contact with vapor). The two “positive plates” are the (connected) halves of the outer cylinder (half of which is in contact with liquid, and half of which is in contact with vapor).

For the cylindrical capacitor

$V=V_{b}-V_{a}=-\int _{a}^{b}{\vec {E}}.d{\vec {l}}=-{\frac {Q}{2\pi \epsilon _{0}l}}\int _{R_{a}}^{R_{b}}{\frac {dR}{R}}={\frac {Q}{2\pi \epsilon _{0}l}}\ln {\frac {R_{a}}{R_{b}}}$

$C={\frac {Q}{V}}={\frac {2\pi \epsilon _{0}l}{\ln(R_{a}/R_{b})}}$

(a)

$C=C_{\textrm {liq}}+C_{\textrm {V}}={\frac {2\pi \epsilon _{0}K_{\textrm {liq}}h}{\ln(R_{a}/R_{b})}}+{\frac {2\pi \epsilon _{0}K_{\textrm {V}}(l-h)}{\ln(R_{a}/R_{b})}}={\frac {2\pi \epsilon _{0}l}{\ln(R_{a}/R_{b})}}\left[(K_{\textrm {liq}}-K_{\textrm {V}}){\frac {h}{l}}+K_{\textrm {V}}\right]=C$

${\frac {h}{l}}={\frac {1}{(K_{\textrm {liq}}-K_{\textrm {V}})}}\left[{\frac {C\ln(R_{a}/R_{b})}{2\pi \epsilon _{0}l}}-K_{\textrm {V}}\right]$

(b)

For the full tank, ${\frac {h}{l}}=1$, for the empty tank ${\frac {h}{l}}=0$

Full=$1.5\times 10^{-9}$F Empty=$1.1\times 10^{-9}$F

Question 2

The kinetic energy of the electrons (provided by the UV light) is converted completely to potential energy at the plate since they are stopped. Use energy conservation to find the emitted speed, taking the 0 of PE to be at the surface of the barium.

${\textrm {KE}}_{\textrm {initial}}={\textrm {PE}}_{\textrm {final}}\rightarrow qV={\frac {1}{2}}mv_{x}^{2}$

$v=1.03\times 10^{6}$m/s

Question 3

(a)

$\Phi _{\textrm {hemisphere}}=\int {\vec {E}}.d{\vec {A}}=\int _{0}^{\pi /2}E\cos \theta (2\pi R^{2}\sin \theta d\theta )$ $2\pi R^{2}E\int _{0}^{\pi /2}\cos \theta \sin \theta d\theta =2\pi R^{2}E({\frac {1}{2}}\sin ^{2}\theta )_{0}^{\pi /2}=\pi R^{2}E$

(b)

Choose a closed gaussian surface consisting of the hemisphere and the circle of radius R at the base of the hemisphere. There is no charge inside that closed gaussian surface, and so the total flux through the two surfaces (hemisphere and base) must be zero. The field lines are all perpendicular to the circle, and all of the same magnitude, and so that flux is very easy to calculate.

$\Phi _{\textrm {circle}}=\int {\vec {E}}.d{\vec {A}}=\int E\cos 180^{\circ }d{\vec {A}}=-E\pi R^{2}$

$\Phi _{\textrm {total}}=0=\Phi _{\textrm {circle}}+\Phi _{\textrm {hemisphere}}=-E\pi R^{2}+\Phi _{\textrm {hemisphere}}\rightarrow \Phi _{\textrm {hemisphere}}=E\pi R^{2}$

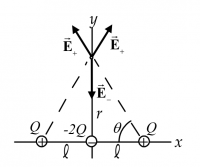
Question 4

$E_{\textrm {net}}=2E_{+}\sin \theta -E_{-}=2{\frac {Q}{4\pi \epsilon _{0}(r^{2}+l^{2})}}{\frac {r}{\sqrt {(r^{2}+l^{2})}}}-{\frac {2Q}{4\pi \epsilon _{0}r^{2}}}$ $={\frac {2Q}{4\pi \epsilon _{0}}}\left[{\frac {r}{(r^{2}+l^{2})^{3/2}}}-{\frac {1}{r^{2}}}\right]$ $={\frac {2Q}{4\pi \epsilon _{0}(r^{2}+l^{2})^{3/2}r^{2}}}\left[r^{3}-(r^{2}+l^{2})^{3/2}\right]$ $={\frac {2Qr^{3}\left[1-\left(1+{\frac {l^{2}}{r^{2}}}\right)^{3/2}\right]}{4\pi \epsilon _{0}r^{5}\left(1+{\frac {l^{2}}{r^{2}}}\right)^{3/2}}}$

using the maclaurin expansion when $r\gg l$ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\textrm{net}=\frac{2Qr^3 \left[1-\left( 1+\frac{l^2}{r^2}\right)^\frac{3}{2}}\right]}{4\pi\epsilon_0 r^5 \left( 1+\frac{l^2}{r^2}\right)^\frac{3}{2}}\approx\frac{2Qr^3 \left[1-\left( 1+\frac{3}{2}\frac{l^2}{r^2}\right)\right]}{4\pi\epsilon_0 r^5 \left( 1+\frac{3}{2}\frac{l^2}{r^2}\right)}} $={\frac {2Qr^{3}\left[\left(-{\frac {3}{2}}{\frac {l^{2}}{r^{2}}}\right)\right]}{4\pi \epsilon _{0}r^{5}\left(1\right)}}$ $=-{\frac {3Ql^{2}}{4\pi \epsilon _{0}r^{4}}}$