Recap of Chapter 25-28

Electric Currents and Resistance

Units
Current	1 A = 1 C/s
Potential difference	1V = 1 J/C
Power	1 W = 1J/s
Resistance	1 $\Omega$ = 1 V/A

• An electric battery serves as a source of nearly constant potential difference.
• Electric current, $I$, refers to the rate of flow of electric charge and is measured in amperes (A): 1 A equals a flow of 1 C/s past a given point.
• The direction of conventional current is that of positive charge flow. In a wire, it is actually negatively charged electrons that move, so they flow in a direction opposite to the conventional current.
• Positive conventional current always flows from a high potential to a low potential.

Ohm's law

• The resistance $R$ of a device is defined through the Ohm’s law

 $V=IR$

• The current $I$ coming from a battery of voltage $V$ depends on the resistance $R$ of the circuit connected to it.
• The resistance $R$ of a wire is inversely proportional to its cross-sectional area $A$, and directly proportional to its length $l$ and to a property of the material called its resistivity $\rho$.

  $R={\frac {\rho l}{A}}$

• Resistivity depends on temperature.

Power

• The rate at which energy is transformed in a resistance R from electric to other forms of energy (such as heat and light) is equal to the product of current and voltage.

  $P=IV$ 

• For Ohmic resistors, Power can also be written as

  $P=I^{2}R={\frac {V^{2}}{R}}$

• SI Unit of power is Watts (W)
• The total electric energy transformed in any device is equals the product of the power and the time during which the device is operated. In SI units, energy is given in joules (1 J = 1 W . s), but electric companies use a larger unit, the kilowatt-hour. (1kWh = $3.6\times 10^{-6}$ J).

Direct and Alternating current

• Electric current can be direct current (dc), in which the current is steady in one direction; or it can be alternating current (ac), in which the current reverses direction at a particular frequency $f$

 $I=I_{0}\sin \omega t$

where $\omega =2\pi f$

• The rms values of sinusoidally alternating currents and voltages are

 $I_{\textrm {rms}}={\frac {I_{0}}{\sqrt {2}}}$ and $V_{\textrm {rms}}={\frac {V_{0}}{\sqrt {2}}}$

• The peakvalues of the current and voltage are $I_{0}$ and $V_{0}$
• The power relationship, $P=IV=I^{2}R={\frac {V^{2}}{R}}$, is valid for the average power in alternating currents when the rms values of V and I are used.

Microscopic view of the current

• Current density ${\vec {j}}$ is the current per cross-sectional area.
• From a microscopic point of view, the current density is related to the number of charge carriers per unit volume, $n$, their charge, $q$, and their drift velocity, ${\vec {v}}_{d}$ , by

  ${\vec {j}}=nq{\vec {v}}_{d}$

• conductivity $\sigma$ is the inverse of resistivity

$\sigma ={\frac {1}{\rho }}$

• The electric field within a wire is related to ${\vec {j}}$

  ${\vec {j}}=\sigma {\vec {E}}$

DC Circuits

emf and internal resistance

• A device that transforms another type of energy into electrical energy is called a source of emf ${\mathcal {E}}$. The emf is the potential difference determined by the chemical reactions in the battery and equals the terminal voltage when no current is drawn.
• A battery behaves like a source of emf in series with an internal resistance.
• When a current is drawn, the voltage at the battery’s terminals is less than its emf by an amount equal to the potential decrease $Ir$ across the internal resistance.

Resistances in series and in parallel

• When resistances are connected in series (end to end in a single linear path), the equivalent resistance is the sum of the individual resistances.

 $R_{\textrm {eq}}=R_{1}+R_{2}+\cdots$

• When resistors are connected in parallel, the reciprocal of the equivalent resistance equals the sum of the reciprocals of the individual resistances:

 ${\frac {1}{R_{\textrm {eq}}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots$

Kirchoff's Rules

• Kirchhoff’s junction rule is based on conservation of electric charge and states that the sum of all currents entering any junction equals the sum of all currents leaving that junction.
• Kirchhoff’s loop rule, is based on conservation of energy and states that the algebraic sum of the changes in potential around any closed path of the circuit must be zero.

Applying the Kirchoff's Rules

• Label the current in each separate branch of the given circuit with a different subscript, such as $I_{1}$ , $I_{2}$ , $I_{3}$.
  • Each current refers to a segment between two junctions.
  • Choose the direction of each current, using an arrow. The direction can be chosen arbitrarily: if the current is actually in the opposite direction, it will come out with a minus sign in the solution.
• Identify the unknowns. You will need as many independent equations as there are unknowns. You may write down more equations than this, but you will find that some of the equations will be redundant (that is, not be independent in the sense of providing new information).
  • You may use V = IR for each resistor, which sometimes will reduce the number of unknowns.
• Apply Kirchhoff’s junction rule at one or more junctions.
• Apply Kirchhoff’s loop rule for one or more loops: follow each loop in one direction only. Pay careful attention to subscripts, and to signs:
  • For a resistor, apply Ohm’s law; the potential difference is negative (a decrease) if your chosen loop direction is the same as the chosen current direction through that resistor; the potential difference is positive (an increase) if your chosen loop direction is opposite to the chosen current direction.
  • For a battery, the potential difference is positive if your chosen loop direction is from the negative terminal toward the positive terminal; the potential difference is negative if the loop direction is from the positive terminal toward the negative terminal.
• Solve the equations algebraically for the unknowns. Be careful when manipulating equations not to err with signs. At the end, check your answers by plugging them into the original equations, or even by using any additional loop or junction rule equations not used previously.

RC Circuits

• A RC circuit contains a resistor R in series with a capacitance C.

Charging the capacitor

• Charging a capacitor with a DC emf: the voltage across the capacitor rises gradually in time characterized by an exponential of the form

  $V(t)={\mathcal {E}}(1-e^{-t/RC})$

• The time it takes for the voltage to reach 63 percent of its maximum value is called the time constant $\tau$

  $\tau =RC$

• The current through the resistor decreases as

  $I(t)=I_{0}e^{-t/RC}$

Discharging the capacitor

• When discharging, the voltage across the capacitor drops to 37 percent of its initial value in $\tau$

  $\tau =RC$

• The charge and potential difference across the capacitor decreases as

  $V(t)=V_{0}e^{-t/RC}$   $Q(t)=Q_{0}e^{-t/RC}$

Magnetism

• A magnet has two poles, north and south. The north pole is that end which points toward geographic north when the magnet is freely suspended.
• Like poles of two magnets repel each other, whereas unlike poles attract.
• The SI unit for magnetic field is the tesla (T).
• Electric currents produce magnetic fields.
• A magnetic field exerts a force on an electric current. The force on an infinitesimal length of wire $d{\vec {l}}$ carrying a current $I$ in a magnetic field ${\vec {B}}$ is

  $d{\vec {F}}=Id{\vec {l}}\times {\vec {B}}$

• If the field ${\vec {B}}$ is uniform over a straight length of wire, the above formula reads

  ${\vec {F}}=I{\vec {l}}\times {\vec {B}}$  and  $\left|{\vec {F}}\right|=F=IlB\sin \theta$

where $\theta$ is the angle between magnetic field ${\vec {B}}$ and the wire. The direction of the force is perpendicular to the wire and to the magnetic field, and is given by the right-hand rule.

• Similarly, a magnetic field ${\vec {B}}$ exerts a force on a charge $q$ moving with velocity ${\vec {v}}$

  ${\vec {F}}=q{\vec {v}}\times {\vec {B}}$ with magnitude $F=qvB\sin \theta$ 

where $\theta$ is the angle between magnetic ${\vec {B}}$ and ${\vec {v}}$.

• The path of a charged particle moving perpendicular to a uniform magnetic field is a circle.

• If both electric and magnetic fields (${\vec {E}}$ and ${\vec {B}}$) are present, the force on a charge $q$ moving with velocity ${\vec {v}}$ is

  ${\vec {F}}=q{\vec {E}}+q{\vec {v}}\times {\vec {B}}$ with magnitude $F=qvB\sin \theta$ 

• The magnetic dipole moment of a loop is

  ${\vec {\mu }}=NI{\vec {A}}$

• • $N$ is the number of coils carrying current $I$ in the loop
  • ${\vec {A}}$ is a vector perpendicular to the plane of the loop (use right-hand rule, fingers along current in loop) and has magnitude equal to the area of the loop.

• The torque ${\vec {\tau }}$ on a current loop in a magnetic field ${\vec {B}}$ is

  ${\vec {\tau }}={\vec {\mu }}\times {\vec {B}}$

• The measurement of the charge-to-mass ratio (e/m) of the electron was done using magnetic and electric fields. The charge e on the electron was first measured in the Millikan oil-drop experiment and then its mass was obtained from the measured value of the e/m ratio.
• In the Hall effect, moving charges in a conductor placed in a magnetic field are forced to one side, producing an emf between the two sides of the conductor.

Sources of Magnetic Field

• The magnetic field $B$ at a distance $r$ from a long straight wire is directly proportional to the current $I$ in the wire and inversely proportional to $r$:

 $B={\frac {\mu _{0}}{2\pi }}{\frac {I}{r}}$

• The magnetic field lines are circles centered at the wire.
• The force that one long current-carrying wire exerts on a second parallel current-carrying wire 1m away serves as the definition of the ampere unit, and ultimately of the coulomb as well.
• Ampère’s law states that the line integral of the magnetic field ${\vec {B}}$ around any closed loop is equal to $\mu _{0}$ times the total net current $I_{\textrm {encl}}$ enclosed by the loop:

  $\oint {\vec {B}}.d{\vec {l}}=\mu _{0}I_{\textrm {encl}}$

• Magnetic field inside a long tightly wound solenoid is

  $B=\mu _{0}nI$     $n$:Number of loops per length $I$:current

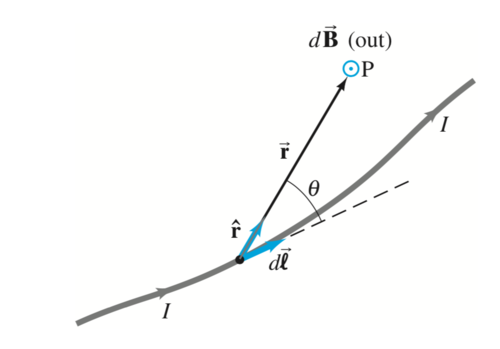
• The Biot-Savart law is useful for determining the magnetic field due to a known arrangement of currents.

   $d{\vec {B}}={\frac {\mu _{0}I}{4\pi }}{\frac {d{\vec {l}}\times {\hat {r}}}{r^{2}}}$
  
   $d{\vec {B}}$ is the contribution to the total field at some point $P$ due to a current $I$ along an infinitesimal length $d{\vec {l}}$ of its path.
   ${\hat {r}}$ is the unit vector along the direction of the displacement vector $d{\vec {r}}$ from $d{\vec {B}}$ to $P$. 

• The total field ${\vec {B}}$ will be the integral over all $d{\vec {B}}$ .