(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Problem
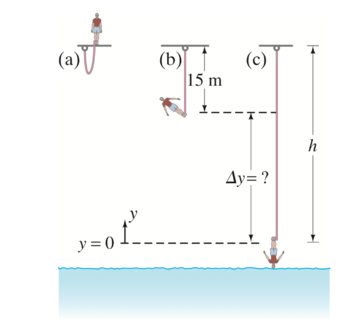
Chris jumps off a bridge with a bungee cord (a heavy stretchable cord) tied around his ankle. He falls for 15 m before the bungee cord begins to stretch. Chris’s mass is 75kg and we assume the cord obeys Hooke’s law,  , with
, with  50 N/m. If we neglect air resistance, estimate how far below the bridge Chris’s foot will be before coming to a stop. Ignore the mass of the cord (not realistic, however) and treat Chris as a particle.
50 N/m. If we neglect air resistance, estimate how far below the bridge Chris’s foot will be before coming to a stop. Ignore the mass of the cord (not realistic, however) and treat Chris as a particle.
Solution
The only forces acting on the bungee jumper are gravity and the elastic force from the bungee cord, so the jumper’s mechanical energy is conserved. Let the lowest point of the jumper’s
motion be the zero location for gravitational potential energy ( y = 0). The zero location for elastic potential energy is the point at which the bungee cord begins to stretch. We have  ,
,  ,
,  , and the amount of stretch of the cord
, and the amount of stretch of the cord  . Solve for
. Solve for  .
.






since