Random phase approximation (RPA) is an important and widely used approximation in condensed matter physics, especially when calculating the linear response of electrons. It accounts for the microscopic quantum mechanical interactions between electrons using weak screened Coulomb interaction.  It was first introduced by David Bohm and David Pines as an important result in a series of seminal papers of 1952 and 1953 [2-4].

In the RPA, electrons are assumed to respond only to the total electric potential $V(\bf r)$ which is the sum of the external perturbing potential $V_\text{ext}(\bf r)$ and a screening potential $V_\text{sc}(r)$. The external perturbing potential is assumed to oscillate at a single frequency $\omega$, so a self-consistent field (SCF)  approach is possible giving a dynamic dielectric function denoted by $\epsilon_\text{RPA}(\bf k, \omega)$ (5) .

The assumption in RPA is that the contribution to the dielectric function from the total electric potential is assumed to average out so that only the potential at wave vector $\bf k$ contributes. This is what is meant by the random phase approximation. The resulting dielectric function correctly predicts a number of properties of the electron gas, including plasmons (see Mahan's Many-Particle Physics).

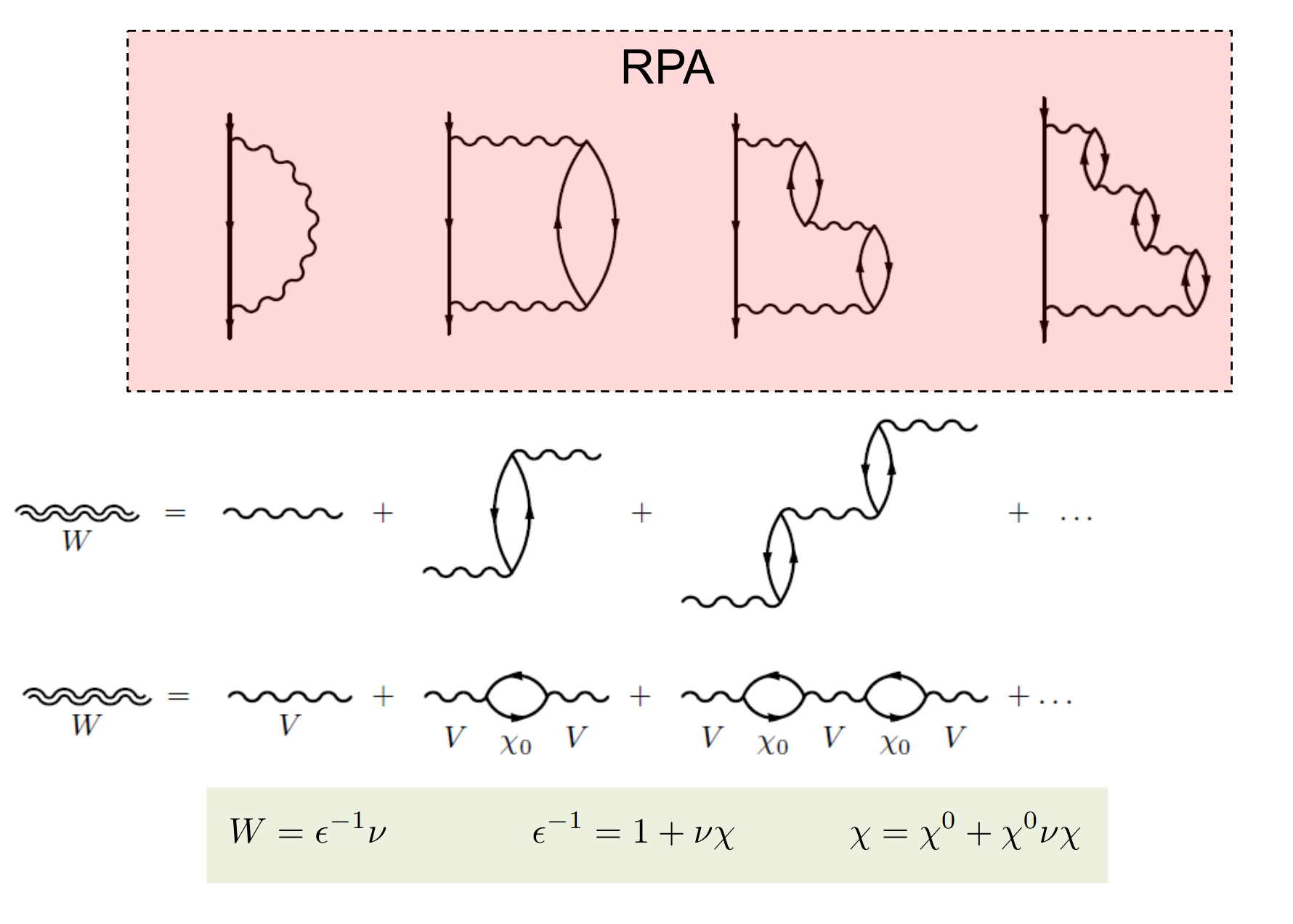
RPA as a diagrammatic summation

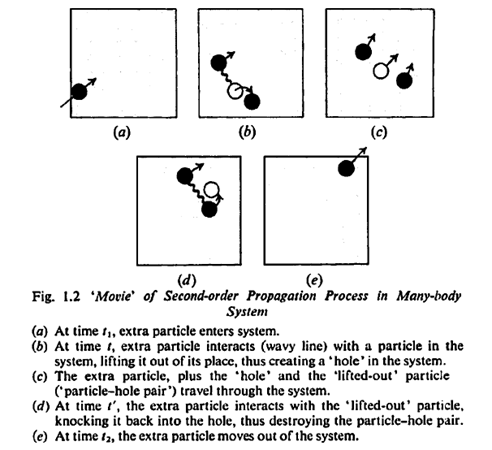
The single particle propagator for a system of many interacting particles can be dissected as a series of virtual events. (a) depicts a free propagation without interaction. The event in (b) depicts a ‘second-order’ propagation process (a process with two interactions).

A sequence of events means we need a time axis. Due to time reversal symmetry, electrons move forward, and holes move backward. By convention, "up" is the forward time.

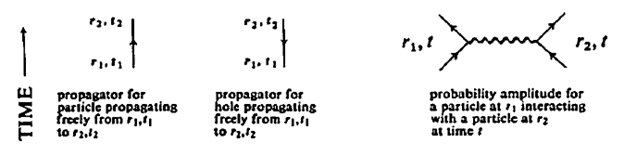
The probability amplitude attached for the above sequence of events can be represented by the diagram:

This diagram is called the self-energy part because it shows the particle interacting with itself via the particle-hole pair it created in the many-body medium.

The process that involve only the one interaction is called the first order processes

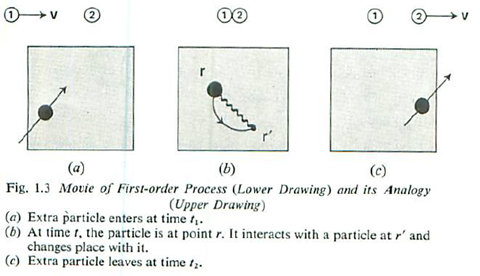
The events above depict the incoming electron at point $r$ interacting with another electron at point $r^\prime$ and the propagation of that electron instead. In diagrammatic language it is depicted as an open oyster diagram.

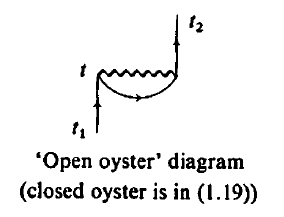
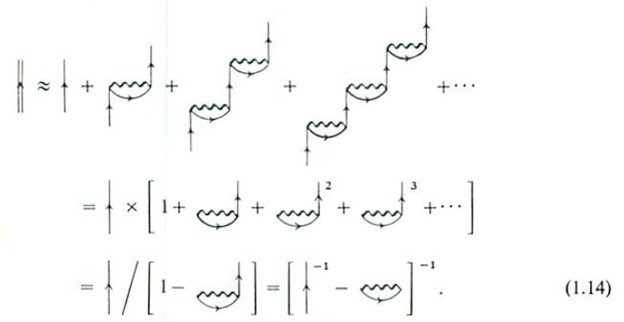
If only these kind of interactions are more important, we can write the total propagator as a sum of open oyster diagrams.

If ring diagrams (particle-hole pair bubbles) are added in the sum, the sum gives the random phase approximation (RPA).

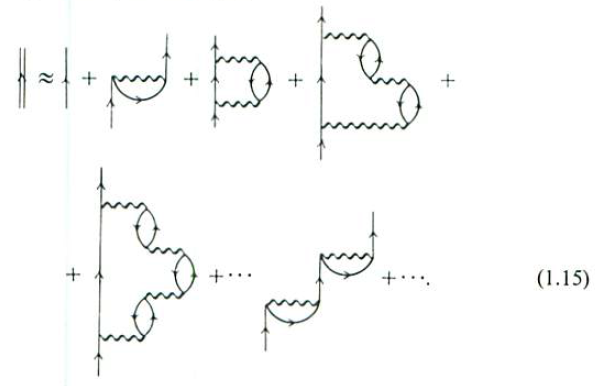
The summation above can be traced back to the famous paper of Murray Gell-Mann and Keith Brueckner which showed that the RPA can be derived from a summation of leading-order chain Feynman diagrams in a dense electron gas.

Obtaining RPA screening term from DFT

The Adler-Wiser formula [7] enables the calculation of bubble diagrams from DFT.

In terms of Bloch functions, $\chi^0$  can be written as
$$\begin{multline} \chi^0_{G,G^\prime}(\mathbf{q}, \omega)=\frac{1}{\Omega}\sum_{nn^\prime \bf k} 2\omega_{\mathbf{ k}} (f_{n^\prime \mathbf{k+q}}-f_{n^\prime \mathbf{k}})\\ \times\frac{\left\langle \psi_{n^\prime \mathbf{k+q}}\left | e^{i\mathbf{(q+G)r}}\right|\psi_{n \mathbf{k}}\right\rangle\left\langle \psi_{n \mathbf{k}}\left | e^{-i\mathbf{(q+G^\prime)r^\prime}}\right|\psi_{n^\prime \mathbf{k+q}}\right\rangle}{\epsilon_{n^\prime \mathbf{k+q}}-\epsilon_{n\mathbf{k}}-\omega-i\eta} \end{multline}$$
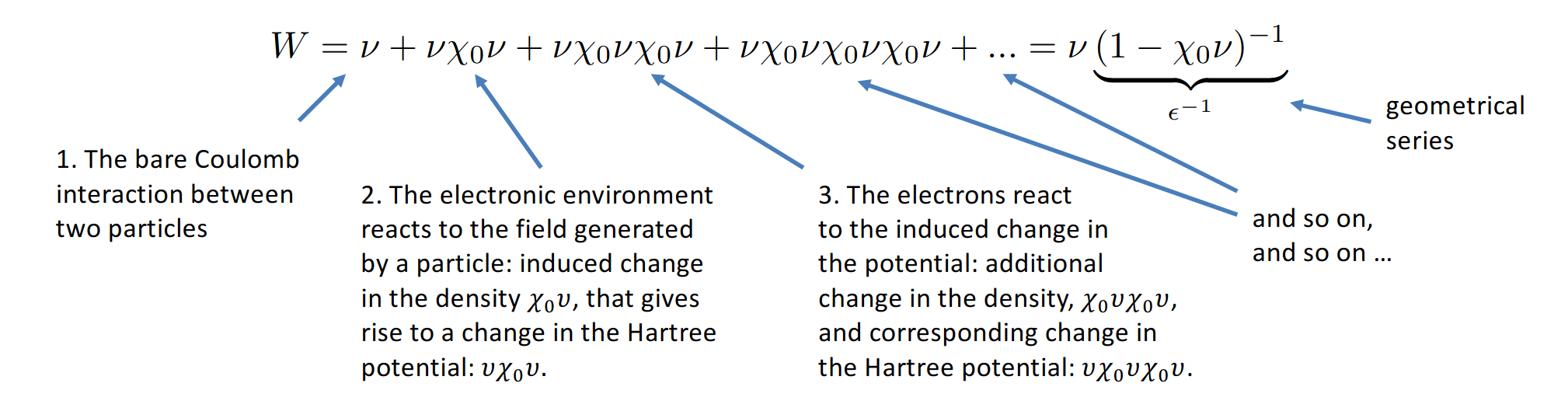
From $\chi^0$, the RPA screened coulomb can be calculated as:
 

References

1. Wikipedia
2. David Bohm and David Pines Phys. Rev. 82, 625 (1951)
3. David Pines and David Bohm Phys. Rev. 85, 338 (1952)
4. David Bohm and David Pines Phys. Rev. 92, 609 (1953)
5. H. Ehrenreich and M. H. Cohen Phys. Rev. 115, 786 (1959)
6. Murray Gell-Mann and Keith A. Brueckner Phys. Rev. 106, 364 (1957)
7. Stephen L. Adler Phys. Rev. 126, 413, Nathan Wiser
   Phys. Rev. 129, 62 
8. VASP RPA lecture