105-2019201 Solutions

Question 1

(a)

It is not possible to determine delta-v requirements from conservation of energy by considering only the total energy of the vehicle in the initial and final orbits since energy is carried away in the exhaust. For example, most spacecraft are launched in an orbit with inclination fairly near to the latitude at the launch site, to take advantage of the Earth's rotational surface speed. If it is necessary, for mission-based reasons, to put the spacecraft in an orbit of different inclination, a substantial delta-v is required, though the specific kinetic and potential energies in the final orbit and the initial orbit are equal.

(b)

$a={\frac {F}{m}}=v_{\text{exh}}{\frac {\rho }{m}}$

$\Delta v=\int _{t_{0}}^{t_{1}}v_{\text{exh}}{\frac {\rho }{m}}dt$ $=-\int _{t_{0}}^{t_{1}}v_{\text{exh}}{\frac {1}{m}}{\frac {dm}{dt}}dt$ $=-\int _{m_{0}}^{m_{1}}v_{\text{exh}}{\frac {1}{m}}dm$

$\Delta v=v_{\text{exh}}\ln \left({\frac {m_{0}}{m_{1}}}\right)$

(c)

$F_{T}=v_{\text{exh}}{\frac {-\Delta m}{\Delta t}}$

$v_{\text{exh}}=6805440{\text{N}}{\frac {43{\text{s}}}{1039{\text{kg}}}}=-282{\text{km/s}}$

$\Delta v=v_{\text{exh}}\ln \left({\frac {m_{0}}{m_{1}}}\right)$

$m_{0}=m_{1}\times e^{\frac {v_{\text{exh}}}{\Delta v}}=830{\text{kg}}\times e^{7}=1005932{\text{kg}}$

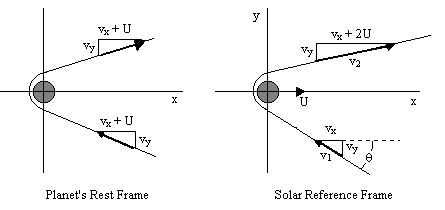
Question 2

(a)

The net effect is almost as if we made an elastic collision at the front of the planet. From the planet's perspective we approached at the speed u+v, and therefore we will also recede at the speed u+v relative to the planet, but the planet is still moving at (virtually) the speed u, so we will be moving at speed 2u+v. This is just like a very small ping pong ball bouncing off a very large basketball.

conservation of kinetic energy and momentum before and after the interaction requires

${\frac {1}{2}}Mu_{1}^{2}+{\frac {1}{2}}mv_{1}^{2}={\frac {1}{2}}Mu_{2}^{2}+{\frac {1}{2}}mv_{2}^{2}$

$Mu_{1}-mv_{1}=Mu_{2}-mv_{2}$

$M(u_{1}-u_{2})(u_{1}+u_{2})=m(v_{2}-v_{1})(v_{2}+v_{1})$

$(u_{1}+u_{2})=-(v_{2}+v_{1})$

$u_{1}=u_{2}=u$ (since the planet is massive, and the change in its speed is negligible)

$v_{2}=-v_{1}-2u$

(b)

Assuming we arrange for a hyperbolic orbit symmetrical about the x axis (with respect to the planet's rest frame), the probe's initial velocity vector with respect to the Sun's rest frame is

$(v_{1})_{x}=-v1\cos \theta$

$(v_{1})_{y}=v1\sin \theta$

$(v_{2})_{x}=v1\cos \theta +2u$

$(v_{2})_{y}=v1\sin \theta$

$v_{2}=v1+2u{\sqrt {1-{\frac {4uv_{1}(1-\cos \theta )}{(v_{1}+2u)^{2}}}}}$