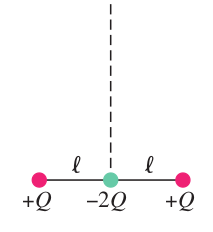106-2018192 Practice for Midterm 1

Disclaimer: These are some random questions which does not have anything to do with the exam. I have no idea or any say about exam questions.

Question 1

XKCD depiction

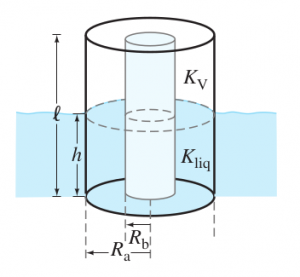
Your team is working on a derivative of F1 engines which can be reused multiple times. You are tasked with finding a way to measure the amount of liquid Nitrogen left in the tank which is responsible for filling the space the oxidizer is spent in a precise and quick manner without igniting a spark in a very very volatile situation. A capacitive level sensor is the way to go. The tank can be modeled as a vertically aligned cylindrical capacitor with outer and inner conductor radii $R_{a}$ and $R_{b}$ , whose length $l$ spans the height of the tank. When a nonconducting liquid fills the tank to a height $h(\leq l)$ from the tank’s bottom, the dielectric in the lower and upper region between the cylindrical conductors is the liquid ($K_{\textrm {liq}}$) and its vapor ($K_{V}$), respectively

(a) Determine a formula for the fraction $F$ of the tank filled by liquid in terms of the level-sensor capacitance $C$.

(b) By connecting a capacitance-measuring instrument to the level sensor, $F$ can be monitored. Assume the sensor dimensions are $l$ = 2.0 m, $R_{a}$ = 5.0 mm, and $R_{b}$ = 4.5 mm. For liquid nitrogen ($K_{\textrm {liq}}$ = 1.4, ($K_{\textrm {V}}$) = 1.0), what values of $C$ (in pF) will correspond to the tank being completely full and completely empty?

Question 2

Barium as plasma source

In order to be able to send a 1.5u cubesat exploration to the heliopause (the boundary between the Sun's solar wind and the interstellar medium), your team is tasked with exploring novel electronic propulsion (EP) methods (such as ion and hall engines). You are experimenting on using Barium and the solar radiation itself. The UV light from the sun provides enough energy to some electrons in barium metal to eject them from the surface at high speed. To measure the maximum energy of such electrons, you place another plate above the barium surface, kept at a negative enough potential, so that the emitted electrons are slowed down and stopped, and return to the barium surface. If the plate voltage is –3.02 V (compared to the barium) when the fastest electrons are stopped, what was the Plate speed of these electrons when they were emitted?

Question 3

The boss without a clue

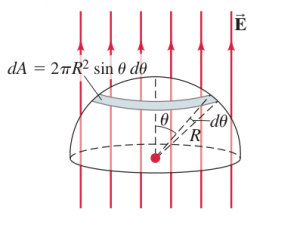
The electronics in the cubesat you are designing are quite vulnerable to intense electric fields when passing through EMIC 'storms' in the van Allen bands. You have to make an estimate of the total flux the cubesat will receive. Your boss insist on a standard procedure which forces you to use a hemisphere of radius $R$ placed in a charge-free region of space where a uniform electric field exists of magnitude $E$ directed perpendicular to the hemisphere’s circular base

(a) Using the definition of $\phi _{E}$ through an “open” surface, calculate (via explicit integration) the electric flux through the hemisphere. (Hint: on the surface of a sphere, the infinitesimal area located between the angles $\theta$ and $\theta +d\theta$ is $dA=(2\pi R\sin \theta )(Rd\theta )=2\pi R^{2}\sin \theta d\theta$)

(b) Choose an appropriate gaussian surface and use Gauss’s law to much more easily obtain the same result for the electric flux through the hemisphere

Question 4

Problematic engine

Unfortunately, your EP engine turns out to behave like one type of electric quadrupole, i.e., it can be modelled as two dipoles placed end to end with their negative charges (say) overlapping; that is, in the center is $-2Q$ flanked (on a line) by a $\pm Q$ to either side. This is due to charging of the barium walls when they eject electrons and prevents effective acceleration of the plasma by the central grid.

Show that the magnitude of the Electric field at points along the perpendicular bisector decreases as $1/r^{4}$ and points towards the negative charge. Measure $r$ from the $-2Q$charge and assume $r\gg l$

hint: Use Maclaurin series.

(bonus) What can you do about this?

Solutions