Chapter 11 Problem 78

Problem

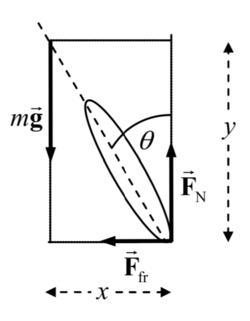
A bicyclist traveling with speed $v=9.2$ m/s on a flat road is making a turn with a radius $r=12$ m. The forces acting on the cyclist and cycle are the normal force ($F_{\text{N}}$) and friction force (${\vec {F}}_{\text{fr}}$) exerted by the road on the tires and $m{\vec {g}}$, the total weight of the cyclist and the cycle.

(a) Explain carefully why the angle $\theta$ the bicycle makes with the vertical must be given by $\tan \theta =F_{\text{fr}}/F_{\text{N}}$ if the cyclist is to maintain balance

(b) Calculate $\theta$ for the values given. [Hint: Consider the "circular" translational motion of the bicycle and rider.]

(c) If the coefficient of static friction between tires and road is $\mu$ 0.65, what is the minimum turning radius?

Solution

(a)

The net torque on the cyclist about an axis through the CM must be zero in order not to fall.

$\sum \tau =F_{\text{N}}x-F_{\text{fr}}y=0$ $\rightarrow {\frac {F_{\text{fr}}}{F_{\text{N}}}}={\frac {x}{y}}=\tan \theta$

(b)

The cyclist is not accelerating vertically, so $F_{\text{N}}=mg$. The cyclist is accelerating horizontally, because he is traveling in a circle. Thus the frictional force must be supplying the centripetal force, so $F_{\text{fr}}=mv^{2}/r$.

$\tan \theta ={\frac {F_{\text{fr}}}{F_{\text{N}}}}={\frac {mv^{2}/r}{mg}}={\frac {v^{2}}{rg}}$ $\rightarrow \theta =\tan ^{-1}{\frac {v^{2}}{rg}}=\tan ^{-1}{\frac {(9.2{\text{m/s}})^{2}}{(12{\text{m}})(9.80{\text{m/s}}^{2})}}=35.74^{\circ }\approx 36^{\circ }$

(c)

The smallest turning radius results in the maximum force. The maximum static frictional force is $F_{\text{fr}}=\mu F_{\text{N}}$

$mv^{2}/r_{\text{min}}=\mu _{s}F_{\text{N}}=\mu _{s}mg$ $\rightarrow r_{\text{min}}={\frac {v^{2}}{\mu g}}={\frac {(9.2{\text{m/s}})^{2}}{(0.65)(9.80{\text{m/s}}^{2})}}=13{\text{ m}}$