Chapter 22 Problem 38

Problem

Charged concentric rods

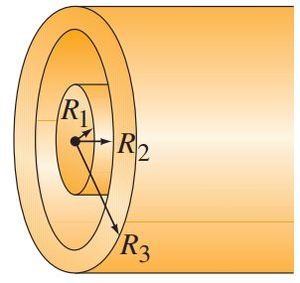
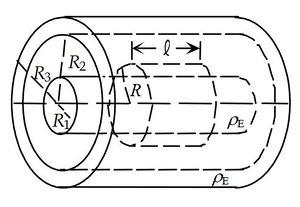
A very long solid nonconducting cylinder of radius $R_{1}$ is uniformly charged with a charge density $\rho _{e}$. It is surrounded by a concentric cylindrical tube of inner radius $R_{2}$ and outer radius $R_{3}$, and it too carries a uniform charge density $\rho _{e}$ Determine the electric field as a function of the distance R from the center of the cylinders for

(a) $0<R<R_{1}$

(b) $R_{1}<R<R_{2}$

(c) $R_{2}<R<R_{3}$

(d) $R>R_{3}$

plot $E$ as a function of $R$ from $R=0$ to $R=20$cm Assume the cylinders are very long compared to $R_{3}$.

Solution

The geometry of this problem is similar to the cylinder example in the course (see lecture notes). So we use the same development.

$\oint {\vec {E}}\cdot d{\vec {A}}=E(2\pi Rl)={\frac {Q_{\textrm {encl}}}{\epsilon _{0}}}\rightarrow E={\frac {Q_{\textrm {encl}}}{2\pi \epsilon _{0}Rl}}$

(a)

The charge enclosed in this range is the volume of the inner rod encompassed times the volume charge density

$E={\frac {Q_{\textrm {encl}}}{2\pi \epsilon _{0}Rl}}={\frac {\rho _{E}\pi R^{2}l}{2\pi \epsilon _{0}Rl}}={\frac {\rho _{E}R}{2\epsilon _{0}}}$

(b)

The only enclosed charge is due to charge of the inner rod.

$E={\frac {Q_{\textrm {encl}}}{2\pi \epsilon _{0}Rl}}={\frac {\rho _{E}\pi R_{1}^{2}l}{2\pi \epsilon _{0}Rl}}={\frac {\rho _{E}R_{1}^{2}}{2\epsilon _{0}R}}$

(c)

The enclosed charge is the total charge of the inner rod, plus the amount enclosed from the outer rod. We can simulate this by considering the outer shell as a positive charge element starting from r=0 and removing the charge due to the cavity by adding a negative charged cylinder up to $R_{2}$. Since we also add the inner cylinder seperately, we end up with charge-no charge-charge setup we intend.

$E={\frac {Q_{\textrm {encl}}}{2\pi \epsilon _{0}Rl}}={\frac {\rho _{E}\pi R_{1}^{2}l+\rho _{E}\left(\pi R^{2}l-\pi R_{2}^{2}l\right)}{2\pi \epsilon _{0}Rl}}={\frac {\rho _{E}\left(R_{1}^{2}+R^{2}-R_{2}^{2}l\right)}{2\epsilon _{0}R}}$

(d)

All the charge is enclosed. We can recycle the previous result. $E={\frac {Q_{\textrm {encl}}}{2\pi \epsilon _{0}Rl}}={\frac {\rho _{E}\left(R_{1}^{2}+R_{3}^{2}-R_{2}^{2}l\right)}{2\epsilon _{0}R}}$

(e)