Problem 1 (on demand)
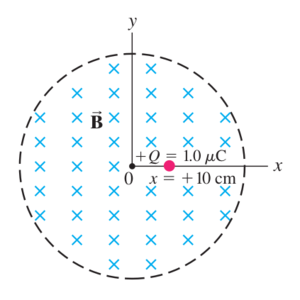
In a circular region, there is a uniform magnetic field  pointing into the page. An xy coordinate system has its origin at the circular region’s center. A free positive point charge
pointing into the page. An xy coordinate system has its origin at the circular region’s center. A free positive point charge  C is initially at rest at a position
C is initially at rest at a position  cm on the x axis. If the magnitude of the magnetic field is now decreased at a rate of
cm on the x axis. If the magnitude of the magnetic field is now decreased at a rate of  T/s, what force (magnitude and direction) will act on
T/s, what force (magnitude and direction) will act on  ?
?
Is this force conservative?
Solution
Remember the Lenz's law

Combining this with the definition of emf, 

i.e. a changing magnetic field produces an electric field.
Choose a circular path centered at the origin with radius 10 cm. By symmetry the electric field is uniform along this path and is parallel to the path. We then use Eq. 29-8 to calculate the electric field at each point on this path. From the electric field we calculate the force on the charged particle.


Since the magnetic field points into the page and is decreasing, Lenz’s law tells us that an induced
circular current centered at the origin would flow in the clockwise direction. Therefore, the initial force on
a positive charge along the positive x-axis would be down, or in the  direction.
direction.
In the electrostatic case, the potential difference between two points is

In the case of a circle since the start and end points are the same,

the relation above,  , tells us that the work done per unit charge around any
closed path is zero (or the work done between any two points is independent of path), which is a property only of a conservative force. But in the nonelectrostatic case, when the electric field is produced by a changing magnetic field, the integral around a closed path is not zero
, tells us that the work done per unit charge around any
closed path is zero (or the work done between any two points is independent of path), which is a property only of a conservative force. But in the nonelectrostatic case, when the electric field is produced by a changing magnetic field, the integral around a closed path is not zero

thus this force is not conservative.
Problem 2
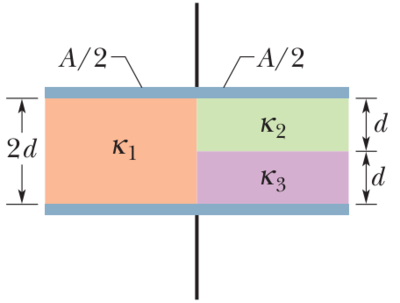
Figure shows a parallel-plate capacitor of plate area  cm 2 and plate separation
cm 2 and plate separation  mm. The left half of the gap is filled with material of dielectric constant
mm. The left half of the gap is filled with material of dielectric constant  ; the top of the right half is filled with material of dielectric constant
; the top of the right half is filled with material of dielectric constant  ; the bottom of the right half is filled with material of dielectric constant
; the bottom of the right half is filled with material of dielectric constant  .What is the capacitance?
.What is the capacitance?
Solution
Let



Note that  and
and  are effectively connected in series, while
are effectively connected in series, while  is effectively connected in parallel with the
is effectively connected in parallel with the  combination. Thus,
combination. Thus,

Plugging in the values

Problem 3
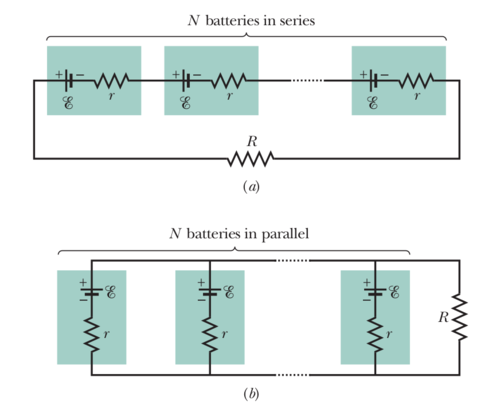
A group of  identical batteries of emf
identical batteries of emf  and internal resistance
and internal resistance  may be connected all in series or all in parallel and then across a resistor
may be connected all in series or all in parallel and then across a resistor  . Show that both arrangements give the same current in
. Show that both arrangements give the same current in  if
if 
Solution
When all the batteries are connected in parallel, the emf is  and the equivalent resistance is
and the equivalent resistance is  so the current is
so the current is

Similarly, when all the batteries are connected in series, the total emf is  and the equivalent resistance is
and the equivalent resistance is  Therefore,
Therefore,

hence when 

Problem 4
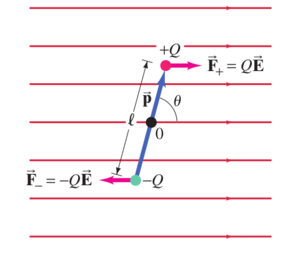
Find an expression for the oscillation frequency of an electric dipole of dipole moment  and rotational inertia
and rotational inertia  for small amplitudes of oscillation about its equilibrium position in a uniform electric field of magnitude
for small amplitudes of oscillation about its equilibrium position in a uniform electric field of magnitude  .
.
Solution

this is a restoring torque, trying to bring the tilted dipole back to its aligned equilibrium position. If the amplitude of the motion is small,  and
and

since this exhibits a simple negative proportionality to the angle of rotation, the dipole oscillates in simple harmonic motion, like a torsional pendulum with torsion constant  .
.



The angular frequency  is given by
is given by

where  is the rotational inertia of the dipole. The frequency of oscillation is
is the rotational inertia of the dipole. The frequency of oscillation is