Problem 1
Two coaxial metal pipes of radii  and
and  (
( ) are lowered vertically into a large oil bath. If a voltage
) are lowered vertically into a large oil bath. If a voltage  is applied between the pipes, show that the top level of the oil between the pipes rises a height
is applied between the pipes, show that the top level of the oil between the pipes rises a height

where  is the dielectric constant and
is the dielectric constant and  is the density of the oil
is the density of the oil
solution
When equilibrium has been reached the battery can be disconnected without effect, so we consider only work done by the electric force and the gravity.

The center of mass of the displaced oil is at height  , thus for a small displacement of the top level of the oil
, thus for a small displacement of the top level of the oil  , the work done by gravity is
, the work done by gravity is

(assuming the lower level of the oil does not change appreciably).
Since the charge  on the pipes remains constant, while their capacitance
on the pipes remains constant, while their capacitance  changes with the presence of oil between them, the work done by the electric force is
changes with the presence of oil between them, the work done by the electric force is

The capacitance per unit length between coaxial cylindrical conductors with a dielectric between them is




so

putting all together:

Problem 2
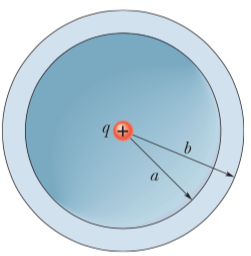
A nonconducting spherical shell of inner radius  =2.00 cm and outer radius
=2.00 cm and outer radius  =2.40 cm has (within its thickness) a positive volume charge density
=2.40 cm has (within its thickness) a positive volume charge density  , where
, where  is a constant and
is a constant and  is the distance from the center of the shell. In addition, a small ball of charge
is the distance from the center of the shell. In addition, a small ball of charge  =45.0 fC is located at that center. What value should
=45.0 fC is located at that center. What value should  have if the electric field in the shell (
have if the electric field in the shell ( ) is to be uniform?
) is to be uniform?
Solution
Since our system possesses spherical symmetry, to calculate the electric field strength, we may apply Gauss’ law and take the Gaussian surface to be in the form of a sphere of radius 
To find an expression for the electric field inside the shell in terms of  and the distance from the center of the shell, choose A so the field does not depend on the distance. We use a Gaussian surface in the form of a sphere with radius
and the distance from the center of the shell, choose A so the field does not depend on the distance. We use a Gaussian surface in the form of a sphere with radius  , concentric with the spherical shell and within it (
, concentric with the spherical shell and within it ( ). Gauss’ law will be used to find the magnitude of the electric field a distance
). Gauss’ law will be used to find the magnitude of the electric field a distance  from the shell center. The charge that is both in the shell and within the Gaussian sphere is given by the integral
from the shell center. The charge that is both in the shell and within the Gaussian sphere is given by the integral  over the portion of the shell within the Gaussian surface. Since the charge distribution has spherical symmetry, we may take
over the portion of the shell within the Gaussian surface. Since the charge distribution has spherical symmetry, we may take  to be the volume of a spherical shell with radius rand infinitesimal thickness
to be the volume of a spherical shell with radius rand infinitesimal thickness  :
:  . Thus,
. Thus,

The total charge inside the Gaussian surface is

The electric field is radial, so the flux through the Gaussian surface is  where E is the magnitude of the field. Gauss’ law yields
where E is the magnitude of the field. Gauss’ law yields

![{\displaystyle E={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{r_{g}^{2}}}+2\pi A-{\frac {2\pi Aa^{2}}{r_{g}^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38b4b7331f3f4f03ecc11c3dc20bf77d1cae313d)
For the field to be uniform, the first and last terms in the brackets must cancel. They do if  or
or  . With
. With  m and
m and  C, we have
C, we have  C/m
C/m



































![{\displaystyle E={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{r_{g}^{2}}}+2\pi A-{\frac {2\pi Aa^{2}}{r_{g}^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38b4b7331f3f4f03ecc11c3dc20bf77d1cae313d)




