Difference between revisions of "105-2019201 Practice"
(→(c)) |
|||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | + | == How to break free from the Sun (The journey of Voyager 1 part 1) == | |
| + | [[File:105-2019201-head.jpg|500px|center|diagram]] | ||
| + | Mariner-Jupiter-Saturn 1977 Spacecraft Artwork, 1975 | ||
| + | NASA and JPL initially referred to what became the Voyagers as the Mariner-Jupiter-Saturn 1977 Project. The two Voyagers were advanced versions of the Mariner-class spacecraft that JPL had flown successfully to Venus, Mars, and Mercury. Shown here is a 1975 JPL artist's rendering of Voyager after encountering Jupiter and, after a gravity assist, approaching Saturn. | ||
===Question 1=== | ===Question 1=== | ||
Delta-v (literally "change in velocity"), symbolised as ∆v and pronounced delta-vee, as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such as launch from, or landing on a planet or moon, or in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of the vehicle. | Delta-v (literally "change in velocity"), symbolised as ∆v and pronounced delta-vee, as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such as launch from, or landing on a planet or moon, or in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of the vehicle. | ||
| Line 10: | Line 13: | ||
As a simple example, take a conventional rocket which achieves thrust by burning fuel. Delta-v is the change in velocity that can be achieved by burning that rocket's entire fuel load. | As a simple example, take a conventional rocket which achieves thrust by burning fuel. Delta-v is the change in velocity that can be achieved by burning that rocket's entire fuel load. | ||
| − | ===(a)=== | + | ====(a)==== |
Is it possible to calculate delta-v requirements of an orbital maneuver from conservation of energy by considering only the total energy of the vehicle in the initial and final orbits? | Is it possible to calculate delta-v requirements of an orbital maneuver from conservation of energy by considering only the total energy of the vehicle in the initial and final orbits? | ||
| − | ===(b)=== | + | ====(b)==== |
Orbit maneuvers are made by firing a thruster to produce a reaction force acting on the spacecraft. The size of this force will be | Orbit maneuvers are made by firing a thruster to produce a reaction force acting on the spacecraft. The size of this force will be | ||
| Line 20: | Line 23: | ||
<math>F_T=v_\text{exh}\rho</math> | <math>F_T=v_\text{exh}\rho</math> | ||
| − | where <math>v_\text{exh}</math> is the velocity of the exhaust gas in rocket frame and <math>\rho=\frac{dm}{dt}</math> is the propellant flow rate to the combustion chamber. | + | where <math>v_\text{exh}</math> is the velocity of the exhaust gas in rocket frame and <math>\rho=-\frac{dm}{dt}</math> is the propellant flow rate to the combustion chamber. |
Assuming <math>v_\text{exh}</math> to be a constant not depending on the amount of fuel left prove the ∆v is given by Tsiolkovsky rocket equation. | Assuming <math>v_\text{exh}</math> to be a constant not depending on the amount of fuel left prove the ∆v is given by Tsiolkovsky rocket equation. | ||
| Line 27: | Line 30: | ||
where <math>m_0</math> is the initial mass of the spacecraft (before the thrust), and <math>m_1</math> is the final mass of the spacecraft (after the thrust). | where <math>m_0</math> is the initial mass of the spacecraft (before the thrust), and <math>m_1</math> is the final mass of the spacecraft (after the thrust). | ||
| + | |||
| + | ====(c)==== | ||
| + | If the heliocentric (i.e. with respect to sun) escape speed required to escape solar system orbiting with earth is around 40 km/s, what is the required amount of fuel to achieve this task without gravity assist? | ||
| + | |||
| + | (Assuming Voyager had kept its initial booster which produced 6805440 N in 43 seconds by burning 1039 kg of solid fuel, and the Voyager mission module is 830 Kg) | ||
| + | |||
| + | How would you propose to make a better interstellar engine? | ||
| + | |||
| + | ===Question 2=== | ||
| + | [[File:105-2019201-q31.png|500px|center|diagram]] | ||
| + | [[File:105-2019201-q32.gif|300px|center|diagram]] | ||
| + | |||
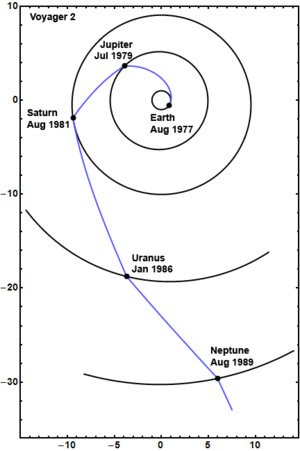
| + | Gravity assistance can be used to accelerate a spacecraft, that is, to increase or decrease its speed or redirect its path. The "assist" is provided by the motion of the gravitating body as it pulls on the spacecraft. The gravity assist maneuver was first used in 1959 when the Soviet probe Luna 3 photographed the far side of Earth's Moon and it was used by interplanetary probes from Mariner 10 onward, including the two Voyager probes' notable flybys of Jupiter and Saturn. | ||
| + | |||
| + | |||
| + | ===(a)=== | ||
| + | |||
| + | [[File:105-2019201-q34.png|200px|center|diagram]] | ||
| + | |||
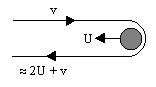
| + | How can you model the "gravity assist"? What are the conserved quantities? | ||
| + | |||
| + | |||
| + | ===(b)=== | ||
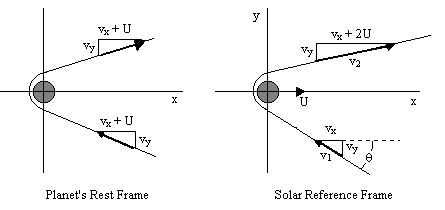
| + | Proove the "gravity assistance" a probe will receive from a planet moving with speed <math>u</math> is | ||
| + | |||
| + | <math>v_2=v_1+2u\sqrt{1-\frac{4uv_1 (1-\cos\theta)}{(v_1-2u)^2}}</math> | ||
| + | |||
| + | assuming as the probe approaches, the axis of motion of the planet is the x axis, and the perpendicular direction (in the orbital plane) is the y axis. The probe is initially moving with a speed <math>v_1</math> relative to the solar reference frame, in a direction approaching the oncoming planet at an angle θ, and leaves with <math>v_2</math>. | ||
| + | |||
| + | [[File:105-2019201-q33.png|500px|center|diagram]] | ||
| + | |||
| − | |||
<math></math> | <math></math> | ||
<math></math> | <math></math> | ||
Latest revision as of 00:35, 23 December 2019
How to break free from the Sun (The journey of Voyager 1 part 1)
Mariner-Jupiter-Saturn 1977 Spacecraft Artwork, 1975 NASA and JPL initially referred to what became the Voyagers as the Mariner-Jupiter-Saturn 1977 Project. The two Voyagers were advanced versions of the Mariner-class spacecraft that JPL had flown successfully to Venus, Mars, and Mercury. Shown here is a 1975 JPL artist's rendering of Voyager after encountering Jupiter and, after a gravity assist, approaching Saturn.
Question 1
Delta-v (literally "change in velocity"), symbolised as ∆v and pronounced delta-vee, as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such as launch from, or landing on a planet or moon, or in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of the vehicle.
When rocket thrust is applied in short bursts the other sources of acceleration may be negligible, and ∆v becomes
As a simple example, take a conventional rocket which achieves thrust by burning fuel. Delta-v is the change in velocity that can be achieved by burning that rocket's entire fuel load.
(a)
Is it possible to calculate delta-v requirements of an orbital maneuver from conservation of energy by considering only the total energy of the vehicle in the initial and final orbits?
(b)
Orbit maneuvers are made by firing a thruster to produce a reaction force acting on the spacecraft. The size of this force will be
where is the velocity of the exhaust gas in rocket frame and is the propellant flow rate to the combustion chamber.
Assuming to be a constant not depending on the amount of fuel left prove the ∆v is given by Tsiolkovsky rocket equation.
where is the initial mass of the spacecraft (before the thrust), and is the final mass of the spacecraft (after the thrust).
(c)
If the heliocentric (i.e. with respect to sun) escape speed required to escape solar system orbiting with earth is around 40 km/s, what is the required amount of fuel to achieve this task without gravity assist?
(Assuming Voyager had kept its initial booster which produced 6805440 N in 43 seconds by burning 1039 kg of solid fuel, and the Voyager mission module is 830 Kg)
How would you propose to make a better interstellar engine?
Question 2
Gravity assistance can be used to accelerate a spacecraft, that is, to increase or decrease its speed or redirect its path. The "assist" is provided by the motion of the gravitating body as it pulls on the spacecraft. The gravity assist maneuver was first used in 1959 when the Soviet probe Luna 3 photographed the far side of Earth's Moon and it was used by interplanetary probes from Mariner 10 onward, including the two Voyager probes' notable flybys of Jupiter and Saturn.
(a)
How can you model the "gravity assist"? What are the conserved quantities?
(b)
Proove the "gravity assistance" a probe will receive from a planet moving with speed is
assuming as the probe approaches, the axis of motion of the planet is the x axis, and the perpendicular direction (in the orbital plane) is the y axis. The probe is initially moving with a speed relative to the solar reference frame, in a direction approaching the oncoming planet at an angle θ, and leaves with .