Difference between revisions of "106-2018192 Practice for Midterm 1"
| Line 1: | Line 1: | ||
| + | '''Disclaimer:''' These are some random questions which does not have anything to do with the exam. I have no idea or any say about exam questions. | ||
==Question 1== | ==Question 1== | ||
| − | [[File:106practice1Q1F1.png|thumb|right| | + | [[File:106practice1Q1F1.png|thumb|right|XKCD depiction of Saturn V's lower stage]] |
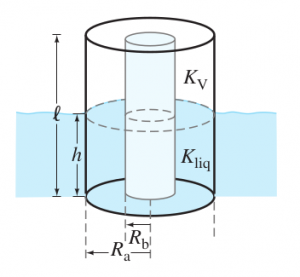
Your team is working on Saturn V's F1 engines. You are tasked with finding a way to measure the amount of liquid Nitrogen left in the tank which is responsible for filling the space the oxidizer is spent in a precise and quick manner without igniting a spark in a very very volatile situation. A capacitive level sensor is the way to go. The tank can be modeled as a vertically aligned cylindrical capacitor with outer and inner conductor radii <math>R_a</math> and <math>R_b</math> , whose length <math>l</math> spans the height of the tank. When a nonconducting liquid fills the tank to a height <math>h(\leq l)</math> from the tank’s bottom, the dielectric in the lower and upper region between the cylindrical conductors is the liquid (<math>K_{\textrm{liq}}</math>) and its vapor (<math>K_V</math>), respectively | Your team is working on Saturn V's F1 engines. You are tasked with finding a way to measure the amount of liquid Nitrogen left in the tank which is responsible for filling the space the oxidizer is spent in a precise and quick manner without igniting a spark in a very very volatile situation. A capacitive level sensor is the way to go. The tank can be modeled as a vertically aligned cylindrical capacitor with outer and inner conductor radii <math>R_a</math> and <math>R_b</math> , whose length <math>l</math> spans the height of the tank. When a nonconducting liquid fills the tank to a height <math>h(\leq l)</math> from the tank’s bottom, the dielectric in the lower and upper region between the cylindrical conductors is the liquid (<math>K_{\textrm{liq}}</math>) and its vapor (<math>K_V</math>), respectively | ||
(a) Determine a formula for the fraction <math>F</math> of the tank filled by liquid in terms of the level-sensor capacitance <math>C</math>. | (a) Determine a formula for the fraction <math>F</math> of the tank filled by liquid in terms of the level-sensor capacitance <math>C</math>. | ||
| + | |||
(b) By connecting a capacitance-measuring instrument to the level sensor, <math>F</math> can be monitored. Assume the sensor dimensions are <math>l</math> = 2.0 m, <math>R_a</math> = 5.0 mm, | (b) By connecting a capacitance-measuring instrument to the level sensor, <math>F</math> can be monitored. Assume the sensor dimensions are <math>l</math> = 2.0 m, <math>R_a</math> = 5.0 mm, | ||
and <math>R_b</math> = 4.5 mm. For liquid nitrogen (<math>K_{\textrm{liq}}</math> = 1.4, (<math>K_{\textrm{V}}</math>) = 1.0), what values of <math>C</math> (in pF) will correspond to the tank being completely full and completely empty? | and <math>R_b</math> = 4.5 mm. For liquid nitrogen (<math>K_{\textrm{liq}}</math> = 1.4, (<math>K_{\textrm{V}}</math>) = 1.0), what values of <math>C</math> (in pF) will correspond to the tank being completely full and completely empty? | ||
| + | [[File:106practice1Q1F2.png|none|300px|The model for Liquid Nitrogen container]] | ||
| + | ==Question 2== | ||
Revision as of 23:21, 17 March 2019
Disclaimer: These are some random questions which does not have anything to do with the exam. I have no idea or any say about exam questions.
Question 1
Your team is working on Saturn V's F1 engines. You are tasked with finding a way to measure the amount of liquid Nitrogen left in the tank which is responsible for filling the space the oxidizer is spent in a precise and quick manner without igniting a spark in a very very volatile situation. A capacitive level sensor is the way to go. The tank can be modeled as a vertically aligned cylindrical capacitor with outer and inner conductor radii and , whose length spans the height of the tank. When a nonconducting liquid fills the tank to a height from the tank’s bottom, the dielectric in the lower and upper region between the cylindrical conductors is the liquid () and its vapor (), respectively
(a) Determine a formula for the fraction of the tank filled by liquid in terms of the level-sensor capacitance .
(b) By connecting a capacitance-measuring instrument to the level sensor, can be monitored. Assume the sensor dimensions are = 2.0 m, = 5.0 mm, and = 4.5 mm. For liquid nitrogen ( = 1.4, () = 1.0), what values of (in pF) will correspond to the tank being completely full and completely empty?